For those who may have used or want to use my G/T spreadsheet tool I have released an improved version 1.12. This is not a bug fix. Continue reading G/T spreadsheet update (v1.12)
Category: Amateur Radio
An admittance graph for NanoVNA-App
Often one finds that a cartesian plot of the components of admittance (conductance and susceptance) would be a convenient plot in understanding / solving a problem.
Let’s work through an example of designing an antenna shunt match to illustrate.
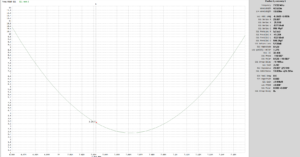
The example is based on measurement of the feed point impedance of a real antenna, an M40 1.2m long vehicle mounted helical whip for the 40m band.
Above is a plot of the VSWR. The minimum VSWR is a bit high, let’s drill down on it. Continue reading An admittance graph for NanoVNA-App
A desk study of the Swan 500CX PA
I recall the arrival of the Swan 500CX in Australia, it was regarded highly and talked up quite forcibly on air by the local agent.
At the time, I was still acquiring the knowledge and skills to analyse the PA design in the 500CX, but I recall lots of on air discussions that were disparaging, but were not convincing.
More recently, I have had occasion to perform a desk study of the 500CX PA.
The Swan 500CX used a pair of 6LQ6, low cost TV sweep valves. From the GE datasheet, the valves are rated at 30 W plate (anode) dissipation. No safe grid 1 current or dissipation is given, so the safe approach is to regard that they must be operated with zero grid current, Class AB1 in this case. Continue reading A desk study of the Swan 500CX PA
Measuring the gain of an antenna by the three antenna method
There are many methods of measuring the gain of an antenna, most of them call for a reference antenna of known gain. This method requires three antennas and does not require knowledge of the gain of any of them, but will find the gain of each of them.
Explanation
Harald Friis gave us the familiar transmission equation: \(\frac{P_r}{P_t}=\frac{A_r A_t}{r^2 \lambda^2}\\\). Continue reading Measuring the gain of an antenna by the three antenna method
On ferrite cored RF broadband transformers and leakage inductance
By broadband transformer, I mean a transformer intended to have nearly nominal impedance transformation over a wide frequency range. That objective might be stated as a given InsertionVSWR over a given frequency range for a stated impedance. eg InsertionVSWR<2 from 3-30MHz with 3200(+j0)Ω load.
These are used in many things, including medium to high power applications such as EFHW matching transformers.
Leakage inductance is the equivalent series inductance due to flux that cuts one winding and not the other, and vice versa. For most simple transformers, the total primary referred leakage inductance is twice the primary leakage inductance. Since the leakage inductance appears in series with the signal path, it causes degradation of nominal impedance transformation, the very simplest approximation of the frequency response is that of a LR circuit.
Above is a Simsmith model of a 1µH total leakage inductance in series with a 50+j0Ω load, the InsertionVSWR is greater than 1.5 above 3MHz.
Is this a common scenario? Continue reading On ferrite cored RF broadband transformers and leakage inductance
Tips and techniques for measuring small RF inductors and transformers
Over more than 50 years, I have measured literally thousands of RF inductors and transformers. This article gives some hints and techniques for making / preparing prototypes for measurement, and measurement.
RF inductors and transformers will often use enameled copper wire (ECW) or some form of insulated wire or coax.
Solid core LAN cables are a good source of small insulated wire for prototyping. The conductor is around 0.5mm, and overall about 0.9mm.
Handy tools
Above, from left to right: Continue reading Tips and techniques for measuring small RF inductors and transformers
A common scheme for narrow band match of an end fed high Z antenna – further explanation
A common scheme for narrow band match of an end fed high Z antenna gives a Simsmith model for the matching arrangement that follows.
The tapped coil could also be considered an autotransformer.
Simsmith model
NanoVNA-H4 v4.3 – initial impressions
I have owned a NanoVNA-H v3.3 for more than two years now. It required some modification to fix a power supply decoupling problem on the mixers, reinforcement of the SMA connectors, replacement of the USB socket, rework of the case so the touch screen worked properly / reliably, and some minor works (eg battery charger chip, bad patch cables, faulty USB cable).
With recent enhancement of firmware to support an SD card, the prospect of stand alone use becomes more practical, so I set about researching and purchase.
It seemed the best option was to buy a ‘genuine’ NanoVNA-H4 v4.3, and I started the search at the recommended (by Hugen) store, Zeenko… but whilst there was a listing for v4.2, there was no v4.3 listing (perhaps it is out of stock). I did find another store selling what they described as a ‘genuine’ NanoVNA-H4 v4.3, but this is a high risk transaction, experience is that Chinese sellers are not to be trusted, and Aliexpress is an unsafe buying platform.
This is one of those concerning transactions where the seller notifies shipment and gives a tracking number hours before the deadline, then a week later change the tracking number (the ‘real’ shipment).
Above, the promo image from the listing. Continue reading NanoVNA-H4 v4.3 – initial impressions
Ambient noise measurement using whip on vehicle – #2 – active antenna electronics
This article continues from Ambient noise measurement using whip on vehicle – #1 – estimate Antenna Factor with a case study for the active antenna electronics.
For this discussion, I will use the amplifier developed at A high performance active antenna for the high frequency band, but applied to the antenna described at Ambient noise measurement using whip on vehicle – #1 – estimate Antenna Factor.
Let’s assume that the antenna + amplifier will be used with a HF receiver with Noise Figure 6dB, Teq=864.5K.
From (Martinsen 2018) Fig 3.8, the amplifier internal noise at the output terminals is -118dBm in 100kHz @ 3.5MHz. That implies that the amplifier Noise Temperature is 857.93K. The amplifier has 6.4dB voltage gain which needs to be subtracted from the AF calculated for unity gain (at the amplifier input terminals). Continue reading Ambient noise measurement using whip on vehicle – #2 – active antenna electronics
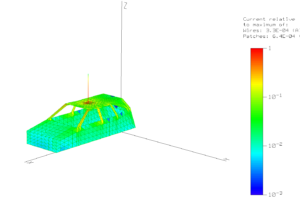
Ambient noise measurement using whip on vehicle – #1 – estimate Antenna Factor
This article lays out a method for estimating the Antenna Factor of a short vertical mounted on the roof of a vehicle for use with a high impedance amplifier for ambient noise measurement at 3.5MHz.
Ambient noise is commonly dominated by man made noise, and it often arrives equally from all directions. For measurement of such noise, the captured power depends on average antenna gain, and so the calculations below focus on gain averaged over the hemisphere.
Antenna Factor is often very convenient for field strength measurement as it relates the external E field strength to the receiver terminal voltage given a certain antenna (system). In fact, given a short vertical terminated by a high impedance amplifier, Antenna Factor is often fairly independent of frequency over several octaves of frequency. Continue reading Ambient noise measurement using whip on vehicle – #1 – estimate Antenna Factor