Ambient noise
Ambient noise usually takes the form of random noise with uniformly distributed power density spectrum, ie the power per Hz of bandwidth is approximately uniform over a wide frequency range.
Ambient noise is often expressed as an ambient noise figure Fam or ambient noise temperature Tam, see ITU-R P.372.
Captured power
There is a direct relationship between ambient noise level and power captured by an antenna system in a given bandwidth.
SDRs and SAs are often calibrated in absolute power units, commonly dBm. SAs often have useful filters to slow the response and help to find the average of a varying signal (usually termed Video Bandwidth VBW).
Any features in an SDR to reduce or cancel noise will probably compromise its use as a measuring instrument.
Bandwidth
SAs as measuring instruments usually have calibrated filter bandwidths (usually termed Resolution Bandwidth RBW). SDRs often have selectable filter bandwidths, but they are often nominal bandwidths rather than Equivalent Noise Bandwidth (ENB), some work may be required to find the actual ENB.
SAs often have useful filters to slow the response and help to find the average of a varying signal (usually termed Video Bandwidth VBW).
Total, internal and external noise power
Both SDRs and SAs have internal noise, and their display is usually calibrated to display the equivalent total power at the input terminals, ie internal and external power, so to arrive at the external power, the internal power must be deducted. That said, if the internal noise is relatively low, it has little influence on the result.
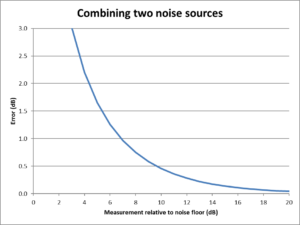
The graph above shows the error in reading the level of two combined noise sources as the level of the higher one. The error is very small when the measurement is more than 20dB above the noise floor, below that the result to be calculated for best accuracy. If for example the noise power displayed on the SDR or SA with 50Ω termination on its input is xdBm, and the antenna noise reads x+10dBm, the true antenna power is x+9.5dBm. Continue reading Can we find the noise power captured by a 50Ω antenna and ambient noise figure using a SDR or spectrum analyser?
Last update: 18th January, 2024, 9:07 AM