Can we find the noise power contributed by a 50Ω antenna using a receiver of known sensitivity?

The article Is a receiver test with different resistors connected it its input terminals meaningful? ended with the question Can we find the noise power contributed by a 50Ω antenna using a receiver of known sensitivity?

The technique depends on the fact that the audio output power of a traditional SSB communications receiver is linearly related to the RF input power (including the equivalent internal noise power) up to the onset of AGC action, which is typically more than 20dB above the equivalent input noise power. Be warned that disabling the AGC does not usually provide a significant extension to the linear range, some stage will overload but you have no warning you have reached that threshold.

For this article, I will use Equivalent Noise Temperature as the sensitivity metric, the reason will become obvious. You can convert various receiver ‘sensitivity’ metrics using the handy Receiver sensitivity metric converter.

Example

Let’s say that a certain receiver has sensitivity specified as 50Ω input, 0.1µV for 10dB S/N. The specifications probably do not give the Equivalent Noise Bandwidth, let us assume it is 2000Hz for this example (appropriate to an SSB telephony receiver but the actual bandwidth is critically important, it can be measured).

Let’s convert that specification to Tr.

Above, Tr is 434K.

So, let’s connect a 50Ω resistor at 290K (room temperature) to the receiver input and measure the audio noise output. The audio noise output power measured is due to total noise input temperature of 290+434=724K.

Now lets connect an antenna instead, verify that there is no ALC action (S meter deflection has not changed) and measure the new audio noise output power. Let’s say the audio noise output power has increased by 5dB, a factor of 3.16 times.

We can calculate the new total noise temperature as 724*3.16=2289K. Deducting the receiver internal Tr, we obtain Text=2289-434=1855K. If the antenna system had an efficiency of say 55%, a loss of 2.6dB, the ambient temperature would be somewhat higher, let’s pick that up later.

Practical issues

Receiver sensitivity

Obviously the method depends on a known receiver, and whilst specifications might be a guide, actual measured NF or Teq, or sensitivity and ENB will give the best accuracy.

Receiver linearity

Receiver linearity is destroyed by ALC action and some other processes such as noise reduction etc.

If the noise power is too high for the receiver’s linear range, use an known attenuator and factor that into the calculations. Some attenuation is likely to be needed below 100MHz.

Calculations

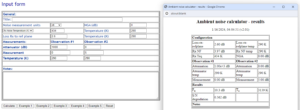
Calculations can become a bit onerous, especially where attenuators are used (including loss to the space interface). This handy calculator makes the task easier and more reliable.

Above, the example worked using Ambient noise calculator. Specified antenna system efficiency of 55% is converted to 2.6dB loss to the reference plane. Observation #1 is specified as a 1000dB attenuator to represent the 50Ω resistor that was used in this discussion. Calculated ambient noise temperature Ta is 3139K, ambient Noise Figure Fa is 10.3dB.