Power standing wave null… more left readers with “homework” to create the Pfwd and Prev traces.
Remember that Pfwd and Prev are interpretations in the context of some Zref of V and I at a point, and that \(P=P_{fwd}-P_{rev}=V_{fwd}I_{fwd}-V_{rev}I_{rev}\) is valid ONLY if Zref is purely real.
So let’s plot Pfwd and Prev wrt:
- Nominal Ro (ie the real part of the nominal Zo of the RG58A/U at 10MHz);
- 50Ω; and
- 75Ω to demonstrate the effect of different contexts, ie Zref.
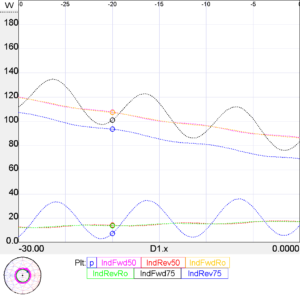
Above IndFwd50 and IndFwdRo are almost coincident (at 10MHz Nominal Ro is very close to 50Ω), as are IndRev50 and IndRevRo. IndFwd75 and IndRev75 are separated from the others. In all cases, the IndFwdxx-IndRevxx is equal to p.
Note that if Zref is close to the line Zo, the shape of Pfwd and Pref are essentially a logarithmic decay in the direction of wave travel with a small superimposed cyclic variation.
If Zref is quite different to line Zo, the exponential element still exists but with a much larger cyclic variation along the line.
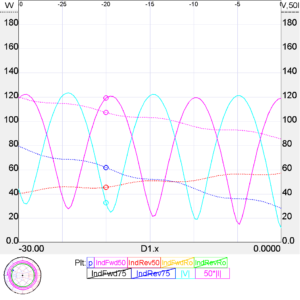
Above is a model of load VSWR=10, and p, Pfwd and Prev wrt 50Ω, and there is still the exponential element and only a relatively small cycle variation.
So, from those we learn that if you were to insert a 50Ω directional wattmeter at various points along a nominal 50Ω line, even with high VSWR, there will be only a small cyclic variation with displacement and the exponential decay will be more significant.
The cyan trace is the voltage along the line, and you may observe that the ratio of max to min near to load is almost 10, VSWR at the load is 10, but measuring the first peak brings a little line loss to bear. The solid magenta curve is 50 times the current (so that it is viewable under the right hand axis scaling).
So, under mismatch there may be a wide variation in voltage and current along the line, but that will not be so apparent on a directional wattmeter which responds to both current and voltage and is sensitive to their phase relationship.
A point for pondering
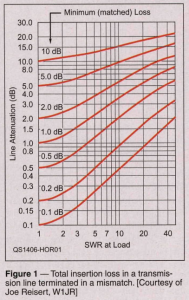
Noting that in this example there is a small standing wave (VSWR=2), and that whilst Matched Line Loss (MLL per meter is uniform along the line, loss under standing waves is not uniform along the line. So the popular graphs that give you (uniform) line loss under standing waves based on VSWR and MLL are unsound, they are an approximation based on usually unstated assumptions.
Downloads
The download below contains the original SimNEC model, and a revised one with the above calcs and traces added.