One sees questions online about measuring a filter response using the NanoVNA.
Let’s discuss filters, the DUT, for a moment.
Filters are usually designed to operate with a given source impedance and given load impedance. It affects the response, and measuring a filter with different source and load impedance that it was designed for, or specified in a test procedure gives invalid results.
This article gives an example measurement of a low pass filter designed for a 50Ω system. The filter is designed for harmonic suppression from a transmitter on the 40m ham band (7-7.2+MHz).
We are interested in measurement of the filter as a two port device.
The VNA as a two port test instrument and suited to measurement of this filter because the impedances match (well, approximately in the pass band).
Above is a block diagram of the signal flow in a two port test with a VNA. An incident wave (Vi) from Port 1 is partially reflected at the DUT input (Vr), and partially transmitted by the DUT to Port 2 (Vt). We make the assumption that there is zero reflection at Port 2 (ie that Port 2 input impedance is 50+j0Ω… though that might not be a very good assumption with low end VNAs… measure it).
Specifically, VNA measurements expressed as S parameters are:
\(s_{11}=\frac{V_r}{V_i}\); and
\(s_{21}=\frac{V_t}{V_i}\).
S parameters are complex quantities, they can be expressed in polar form (magnitude and phase) or rectangular form (real and imaginary parts).
Often just the the magnitude is of interest, and it is often expressed in dB.
Other interesting metrics can be derived:
- \(ReturnLoss_{dB}=-|s_{11}|_{dB}\); and
- \(InsertionLoss_{dB}=-|s_{21}|_{dB}\).
Test configurations
The filter designer may specify one of two common methods of measurement and lineup of filters (or both):
- transmission measurement / lineup; and
- reflection measurement / lineup.
Transmission measurement / lineup
\(|s_{21}|_{dB}=20 \log \frac{V_t}{V_i}\). If the network input impedance is approximately 50+j0Ω, the then \(Gain_{dB} \approx |s_{21}|_{dB}\) and \(TransmissionLoss_{dB} \approx -|s_{21}|_{dB}\).
See Measurement of various loss quantities with a VNA for discussion of cases where input impedance is not very close to 50+j0Ω.
So, lineup instructions might be to adjust to a specified response shape.
Reflection measurement / lineup
Reflection measurement specifications might stipulate a response in terms of ReturnLoss vs frequency.
An example low pass filter (LPF)
The example LPF is one sold by Sotabeams as a transmitter filter in a 50Ω system for the purposes of harmonic suppression, this one is their 40m filter. My own intended use is between 7.0 and 7.2MHz, let’s call that the band of interest (BOI).
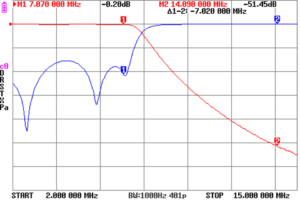
Let’s firstly look at plots based on magnitude of s11 and / or s21.
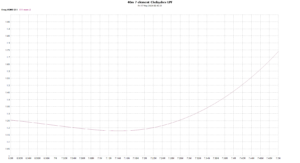
Above is a plot of |s11| and |s21|. Note that |s21| falls off above about 7.2MHz.
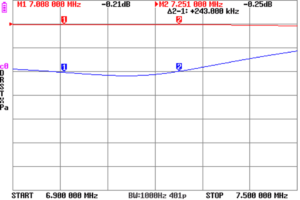
Above is a zoomed in plot of |s11| and |s21| in the 40m band. InsertionLoss (|s21|) is quite low ‘in-band’, and less than 0.21dB over the BOI.
Above is the same plot with the |s11| statistic selected for the marker display. |s11| is moderately low, <-20dB over the BOI.
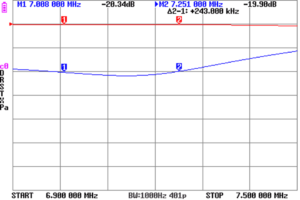
NanoVNA does not (currently) display ReturnLoss, above is a plot of in-band ReturnLoss from NanoVNA-App.
Above is a plot of in-band InsertionVSWR from NanoVNA-App. InsertionVSWR is moderately low, <1.26 over the BOI.
As explained at Measurement of various loss quantities with a VNA InsertionLoss can be disaggregated into to interesting components, InsertionLoss=MismatchLoss+TransmissionLoss. (TransmissionLoss is simply Loss, but let’s use the term TransmissionLoss for clarity in this article.)
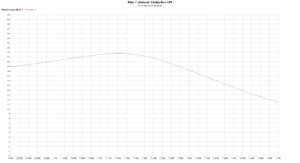
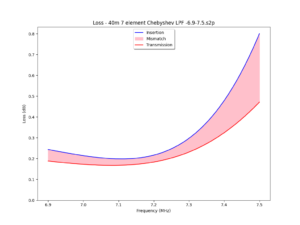
Above is a disaggregation of InsertionLoss into its components over the frequency range 2-15MHz It can be seen that whilst MismatchLoss is quite small below the filter cut off frequency, it becomes quite high in the reject frequency range.
Above is a disaggregation of InsertionLoss into its components over the frequency range 6.9-7.5MHz.
In the BOI, InsertionLoss is less than 0.21dB. TransmissionLoss is less than 0.18dB, which allows us to calculate the heat lost with say 10W input power as \(P_{loss}=P_{in} (1-10^\frac{\text{-TransmissionLoss}}{10})=0.406 \text{ W}\).
Now to phase interpretation.
For some applications, phase response is important. Most commonly, where phase is important, one wants propagation time or delay through the filter to be independent of frequency so that complex waves are not distorted by delay to some frequency components. Constant delay or propagation time means phase proportional to frequency, \(Phase \propto Frequency\).
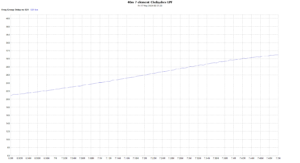
Above is a plot of phase of s21 vs frequency, it is not quite linear, not quite proportional to frequency. A better way to view this is showing GroupDelay (which NanoVNA’s menu tends to call Delay).
Above is a plot of phase of GroupDelay of s21 vs frequency. For a phase linear filter response, GroupDelay would be approximately constant. The response of a filter with critical phase linearity might be specified as limits on GroupDelay over the ‘in-band’ frequency range.
Traps with the NanoVNA and like
The signal emitted by Port 1 may not be a pure sine wave, but a squarish wave. In CW mode where sweeping is suspended, the output is probably not a pure sine wave (as implied by the industry term CW meaning continuous unmodulated sine wave). Hams give a different meaning to CW, and NanoVNA another meaning again.
If the output signal is a complex wave, broadband detectors as often used with Standard Signal Generators and conventional Sweep Generators are not suitable for measurements.
Some kinds of filters require a larger dynamic range than the NanoVNA, eg a repeater duplexor for which you might want to measure rejection notches of over 100dB.
If the filter is not entirely passive, then the output level from the VNA becomes relevant in terms of overload and possibly any form of automatic gain control.
Legacy test setups
50Ω Sweep generator with 50Ω crystal detector
The sweep generator generates a nearly pure sine wave.
The detector (eg HP-423A) terminates the DUT in 50Ω and provides Y voltage to an oscilloscope, the X voltage coming from the sweep generator or possibly the oscilloscope’s internal timebase synchronised to the sweep generator. Detectors often produced a -ve voltage, and the trace on the oscilloscope was ‘right way up’ for gain display.
A VNA may be substituted depending on level requirements, Port 2 provides the 50Ω termination.
50Ω Sweep generator with high impedance detector
The sweep generator generates a nearly pure sine wave.
The detector is high impedance and does not load the filter, so the filter must be loaded with its design load. The detector provides Y voltage to an oscilloscope, the X voltage coming from the sweep generator or possibly the oscilloscope’s internal timebase synchronised to the sweep generator.
It may be possible to design and build a high impedance buffer amplifier (eg FET source follower followed by a BJT emitter follower ahead of Port 2 to make a high impedance probe which will give similar results to the high impedance detector discussed above.