It is easy to become focused on the behavior of a component, but don’t lose sight of the fact that it is but a component of a system where components interact, and the system response is the bigger / more complete picture.
In the article MismatchLoss of severely mismatched EFHW transformer , a caveat stated and restated was:
Transmitters are not necessarily well represented as a Thevenin source, so measurements using such sources (VNA, SA with TG) and application of linear circuit theory are not necessarily applicable.
So, can we estimate a likely system response to a 30+j0Ω load, good 1:49 transformer and modern HF 100W (20dBW) SSB transceiver designed for a nominal 50Ω load?
The following analysis gives a likely solution and it deals with a common implementation where the source is anything but a Thevenin source.
PA VSWR protection
Most transceivers of this type incorporate several PA protection measures, and one of them is commonly to reduce IF gain so that reflected power measured in a directional coupler near the antenna jack is not more than say 4W. This accommodates VSWR up to 1.5 without power reduction due to VSWR protection.
So, with an extreme mismatch, Pref=4W due to the PA protection system.
30+j0Ω load via an ideal 1:49 transformer
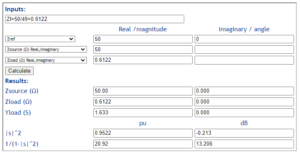
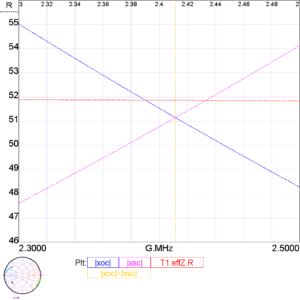
The scenario of 30+j0Ω load if that of the quoted measurement in the previous article, used without comment on its merit.
Lets use the calculation from the previous article, the equivalent case of a 50Ω Thevenin source with load of (30+j0)/49=0.6122+j0Ω.
The quantity 1/(1-|s|^2) is the MismatchLoss, \(MismatchLoss=\frac{P_{fwd}}{P_{fwd}-P_{ref}}=\frac1{1-\frac{P_{ref}}{P_{fwd}}}\) and it is 20.92, so we can calculate that if Pref=4w (by virtue of PA protection), that \(P_{fwd}=\frac{P_{ref}}{0.952}=\frac4{0.952}=4.202 \text{ W}=6.235 \text{ dBW} \). Continue reading MismatchLoss of severely mismatched EFHW transformer – system response