Antenna system resonance and the nanoVNA contained the following:
Relationship between angle of reflection coefficient and angle of impedance
It was stated above that the angle (or phase) of s11 or Γ is not the same as the angle (or phase) of Z.
Given Zo and Γ, we can find θ, the angle of Z.
\(
Z=Z_0\frac{1+\Gamma}{1-\Gamma}\)Zo and Γ are complex values, so we will separate them into the modulus and angle.
\(
\left | Z \right | \angle \theta =\left | Z_0 \right | \angle \psi \frac{1+\left| \Gamma \right | \angle \phi}{1-\left| \Gamma \right | \angle \phi} \\
\theta =arg \left ( \left | Z_0 \right | \angle \psi \frac{1+\left| \Gamma \right | \angle \phi}{1-\left| \Gamma \right | \angle \phi} \right )\)We can see that the θ, the angle of Z, is not simply equal to φ, the angle of Γ, but is a function of four variables: \(\left | Z_0 \right |, \psi , \left| \Gamma \right |, \& \: \phi\) .
It is true that if ψ=0 and φ=0 that θ=0, but that does not imply a wider simple equality. This particular combination is sometimes convenient, particularly when ψ=0 as if often the case with a VNA.
This article offers a simulation of a load similar to a 7MHz half wave dipole.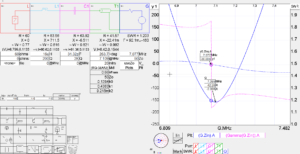
The load comprises L, L1, and C1 and the phase of s11 (or Γ) and phase of Z (seen at the source G) are plotted, along with VSWR. Continue reading Phase of s11 and Z
