(Dunlavy 1967) sets out his description of a wide range tunable transmitting loop antenna and makes a broad efficiency claim of better than 30% (-5.3dB) for his system.
Minimum efficiencies of 30 percent are attainable with practical designs having a diameter of only 5 feet for 3-15 Megahertz coverage.
In a context where extravagant claims are often made for such antennas, his claims warrant review.
Dunlavey gives an example embodiment in approximate terms.
Practical loop designs for use in the range of 2-30 megahertz will utilize copper or aluminum tubular conductors having a diameter of 3 inches to 5 inches. A typical design for 3 to 15 Megahertz operation would be constructed as shown in FIG. 2 with a primary loop 4 having a diameter of about 5 feet and tuned by a high voltage vacuum capacitor 5 having a capacitance range of approximately 25 to l,000 picofarads. The tuned primary loop should be made of aluminum or
copper tubing having a diameter of approximately 4 inches-5 inches. The diameter of the feed loop, which is designated by the reference number 6, for 50 ohms impedance should be approximately l0 inches.
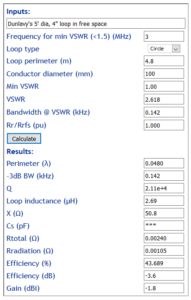
Lets take a perimeter of 4.8m (dia=5′) and copper conductor diameter of 100mm (4″) as the dimensions for further exploration.
Above, Dunlavy’s Figure 5 gives gain relative to a monopole above perfectly conducting ground.
Analysis
Lets deconstruct that a little.
Dunlavy gives an approximate expression for radiation resistance. The expression is a familiar approximation for the radiation resistance of a small loop with uniform current distribution in free space. The expression is not correct for a small loop near a perfectly conducting ground, radiation resistance of a small loop doubles as it approaches a perfectly conducting ground.
Given Dunlavy’s discussion of how he calculates efficiency, it is assumed that the efficiency (and gain) implied by his Figure 5 is for the loop in free space.
The gain of a lossless λ/4 monopole above perfectly conducting ground is 5.14dBi, and a good implementation should have gain very close to the lossless value. The gain of a lossless STL in free space is 1.76dBi. So, at 3MHz Dunlavy gives the gain of the loop as 7dB below the lossless λ/4 monopole above perfectly conducting ground, and efficiency is simply 5.14-1.76-7=-3.6dB (assuming his reference monopole efficiency is almost 0dB).
Above is a model of his loop in free space.
Radiation resistance is calculated to be 0.00105Ω, and as Dunlavy explains, an efficiency of -3.6dB implies a total resistance Rt of Rr/10^(-3.6/10)=0.0024Ω. From that and calculated loop inductance, Q and BW can be calculated. A simpler approach is to juggle the input value for bandwidth to obtain an efficiency of -3.6dB.
So, given Rt and Rr we can calculate total loss resistance for -3.6dB efficiency, Rloss=0.0024-0.00105=1.35mΩ.
Practical loop
We would expect the effective RF resistance at 3MHz of 4.8m of 100mm diameter copper to be 6.9mΩ, and there would be further loss resistance in the tuning capacitor.
A tuning capacitor with Q of 5000 would have an EST of 10mΩ.
Losses in the feed system should be relatively insignificant.
Such a loop in free space would have Rt=0.01795, and with Rr=0.00105, efficiency would be 5.8% or -12.3dB.
Such a loop near real ground would have a different Rr (dependent on height and ground type), and an additional loss element due to energy loss in real ground, and efficiency significantly lower than the -12.3dB for free space.
Conclusions
Dunlavy’s efficiency curve implies a total loss resistance well less than could be practically achieved with 100mm copper conductor and a very good tuning capacitor, overstating efficiency in free space by around 9dB.
Dunlavy’s graph would seem to bear little relation to a practical loop over real ground where radiation resistance is affected by ground reflection and loss in that ground reflection change the result.
References
- Dunlavy, J. Oct 1967. Wide range tunable transmitting loop antenna, US Patent US3588905.