VNA fixture for measuring Zcm of a common mode choke – coax wound discussed issues with common ham practice for measuring coax wound common mode chokes.
The article left readers with some homework:
- Does the same thing occur if the core is wound with twisted pair that is well represented as a uniform two wire transmission line?
- Are the resistors beneficial?
- Do they degrade fixture behavior?
- Then, why are the used so often?
This article addresses those questions.
Does the same thing occur if the core is wound with twisted pair that is well represented as a uniform two wire transmission line?
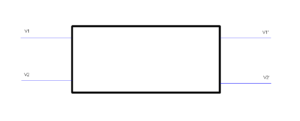
Let’s treat the common mode choke as a black box with two input terminals at left and two output terminals at right with voltages as annotated above.
The common mode voltages at input and output can be calculated, and common mode current calculated for common mode impedance Zcm.
The common mode component of current flows equally in each input terminal.
\(I_c=\frac{\frac{V_1+V_2}{2}-\frac{V_1 \prime+V_2 \prime}{2} }{Z_{cm}}\\\) \(I_c=\frac{V_1-V_1 \prime}{2Z_{cm}}+\frac{V_2-V_2 \prime}{2Z_{cm}}\\\)The last equation contains two terms that can be implemented as impedance elements connected from V1 to V1′ and V2 to V2′, each of value 2Zcm
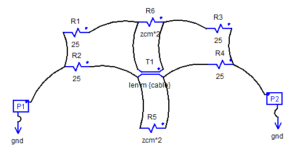
Above is the changed RUSE block for the SimNEC model. The circuit is fully symmetric.
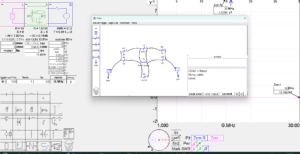
Above is the model of the symmetric twisted pair choke in the fixture with R1-4=25Ω. Observe that the externally calculated Zcm=1.025K+j12.04pΩ, the imaginary component is insignificant and due to computational error, so Zcm=1025 where the real Zcm is 1000.
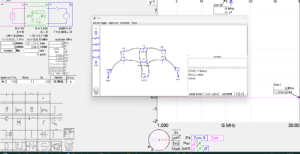
Above, R1-4 are set to zero, observe that externally calculated Zcm=1K-j1.309e-28Ω, the imaginary component is insignificant and due to computational error, so Zcm=1000 which reconciles exactly with the real Zcm being 1000.
Are the resistors beneficial?
No, rather the opposite.
Do they degrade fixture behavior?
Yes.
Then, why are the used so often?
Ask the people doing so… challenge the authors.