Tuning electrical line length using phase of measured s21 – nanoVNA discussed the relationship between phase of s21 and the electrical length of a line section.
An interesting question is the magnitude and phase of the ratio V21 (V at port2 to V at port 1) in the presence of a standing wave.
At first you might answer that the phase difference is exactly that due to the electrical length of the transmission line section, the magnitude might be harder to guess.
There is a simple graphical solution on the Smith chart, yes it was designed to solve this problem.
Recall that the Smith chart is a polar plot of the complex reflection coefficient Γ, so when we plot an impedance point using the R and X scales, we are plotting a vector from the prime centre of the Smith chart, its length being |Γ|=ρ and angle being the angle of Γ.
The voltage at a point on the line is the sum of the forward and reflected waves, its relative magnitude is 1+Γ, known as the Transmission Coefficient. This vector is plotted from the R=0,X=0 point to the impedance of interest.
Lets look at the case of a 50+j0Ω load on a 75Ω line of length 40°.
We will start at the load end of the line, that is the way these problems are solved.
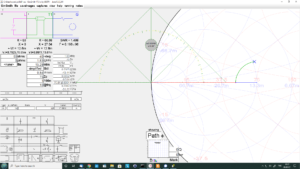
Above is a screenshot of the scenario from Simsmith. I have added a calibrated screen ruler to measure the Transmission Coefficient 1+Γ. 1+Γ=0.8∠0°.
Now lets look at the relationship at the other end of 1+Γ at that end.
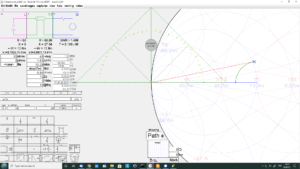
From the screenshot, 1+Γ=0.99∠11.5°. Now recall that the relationship we noted above at the load end is 40° delayed from the source end, ie the phase is -40°. So the ratio \(V_{21}=\frac{V2}{V1}=\frac{0.8∠-40°}{0.99∠11.5°}=0.81∠-51.5°\). Keep in mind that although I used a screen ruler, this is still a graphical solution and accuracy is not as good as a calculation. In fact, calculation gives 0.7943∠-51.71°.
If you were to use a oscilloscope or vector voltmeter to measure the two voltages V1 and V2 and calculated V2/V1, you should get something very close to 0.8∠-52°.
Recall that I said that the Smith chart was designed to solve this problem. I used a screen ruler to measure the 1+Γ vectors, but on a paper Smith chart you might use a protractor and ruler… but lets look at the inbuilt scales.
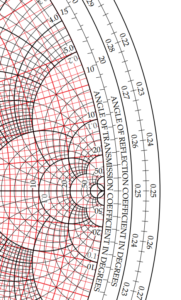
Note the innermost circular scale ANGLE OF TRANSMISSION COEFFICIENT IN DEGREES. The tick marks might look like they are at a strange angle, but they are for measuring the angle of 1+Γ vectors projected from R=0,X=0 to the scale. This scale can be used to measure the angle using only a ruler (or a piece of cotton and dividers for that matter).
The important finding in all of this is the the phase relationship between V2 and V1 under standing waves is not simply equal to the electrical length of the line.
A modified procedure can be followed to find I2/I1, an exercise left to the reader.
The quantities I2/V1 and V2/I1 can be more interesting in some applications.
Conclusions
The ratio V2/V1 can be found, it is not what many people might first guess and the solution goes to the heart of understanding transmission lines.
Last update: 2nd January, 2021, 9:15 AM




