 |
| OwenDuffy.net |
|
This calculator estimates the impedance and equivalent series inductance of circular cross section ferrite toroid cored inductors at HF.
SVN:
The calculator does not do a lot of error checking, if you enter nonsense, it will produce nonsense. NaN means not a number, check the input values.
The model used is of a simple parallel resonant circuit to represent the inductance of the turns, loss due to core losses as implied by complex permeability, and equivalent stray capacitance. The calculator does not model dimensional resonance effects that occur in some ferrite materials (other than to the extent captured by µ', µ'').
Inductors exhibit a self resonance, the effect of which can be estimated by shunting the calculated series R,Xl with an equivalent capacitance, usually in the region of 2 to 10pF (depending on the physical layout, turns spacing etc).
Conductor loss is ignored as for most practical ferrite cored inductors at RF, the core losses dwarf copper loss.
| Input field | Meaning |
| Frequency | The frequency at which to calculate Xl and R |
| OD | OD of the torus |
| ID | ID of the torus |
| µ' | Real part of the complex relative permeability |
| µ'' | Imaginary part of the complex relative permeability |
| Turns | Number of turns |
| Cs | Estimated equivalent stray capacitance |
To calculate the impedance of choke of 11 turns on a FT240-43 core at 3.5MHz, we firstly need to determine µ' and µ'' at 3.6MHz from the manufacturer's data.
 |
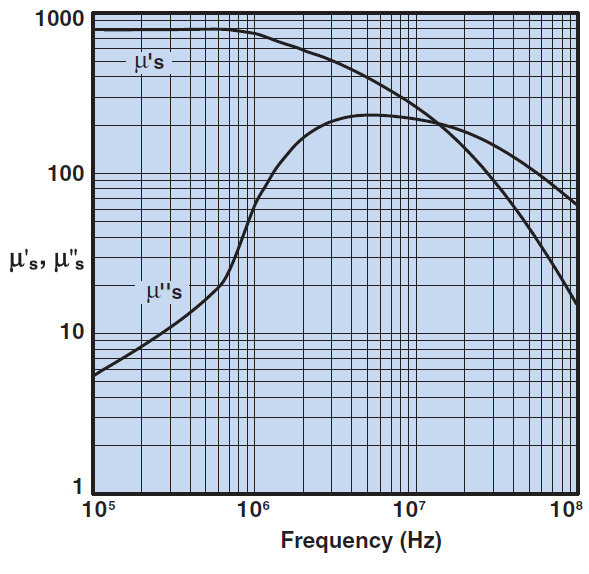
Fig 1 from the Fair-rite data book shows the complex permeability of #43 mix. At 3.6MHz, µ'=470 and µ''=224.
An FT240 core has OD=61mm, ID=35.6mm, Width=12.7mm.
Lets say Cs was 2pF.
Plugging these values into the calculator, you should get Z=998+j1870Ω and Leq=82.7µH (so Q=Xl/R=1.87).
Note that lots of calculators would give a result based on µi, the Initial Permeability at low frequencies, 800 for #43 mix, but the graph shows that such a calculation is only valid up to about 600kHz for #43 material.
| Freq (MHz) | 31 | 43 | 52 | 61 | 67 | 73 | F14 | |||||||
| µi=1500 | µi=800 | µi=250 | µi=125 | µi=40 | µi=2500 | µi=220 | ||||||||
| µ' | µ'' | µ' | µ'' | µ' | µ'' | µ' | µ'' | µ' | µ'' | µ' | µ'' | µ' | µ'' | |
| 1.8 | 1167.2 | 702.1 | 609.8 | 149.3 | 272.3 | 4.0 | 120.3 | 0.3 | 40.6 | 0.1 | 1540.4 | 1315.4 | 219 | 2 |
| 3.6 | 657.7 | 677.9 | 470.2 | 224.0 | 278.7 | 7.8 | 120.6 | 0.6 | 40.3 | 0.1 | 839.9 | 1057.1 | 235 | 4 |
| 7.1 | 359.1 | 476.1 | 332.0 | 228.0 | 305.2 | 73.8 | 123.4 | 1.2 | 40.2 | 0.1 | 457.4 | 803.3 | 265 | 36 |
| 10.1 | 275.3 | 385.3 | 259.7 | 220.4 | 258.2 | 138.7 | 127.4 | 2.1 | 40.3 | 0.1 | 296.7 | 685.7 | 257 | 89 |
| 14.2 | 223.4 | 323.8 | 201.2 | 204.3 | 186.8 | 151.2 | 136.8 | 6.2 | 40.5 | 0.1 | 157.9 | 562.0 | 222 | 111 |
| 18.1 | 187.9 | 284.9 | 159.9 | 189.3 | 150.8 | 138.8 | 150.8 | 20.1 | 40.8 | 0.1 | 86.2 | 458.8 | 189 | 117 |
| 21.2 | 165.2 | 262.4 | 135.3 | 179.4 | 132.2 | 126.8 | 153.7 | 41.5 | 40.9 | 0.1 | 49.4 | 396.2 | 172 | 121 |
| 24.9 | 144.6 | 241.0 | 113.7 | 168.7 | 118.0 | 116.8 | 140.7 | 64.9 | 41.2 | 0.1 | 25.0 | 336.2 | 157 | 124 |
| 28.5 | 129.2 | 224.5 | 97.5 | 158.4 | 107.2 | 109.4 | 124.5 | 76.6 | 41.4 | 0.1 | 8.8 | 289.8 | 146 | 126 |
Table 2 give interpolated values for µ' and µ'' for some common mixes at spot frequencies in the HF ham bands.
The calculator can be applied to powdered iron cores, but differently to ferrite, the complex permeability is not usually published (enter it as zero, and R cannot be calculated), and µ' tends to be less frequency sensitive at HF than most ferrite mixes.
Experience is that measured Q of powdered iron cores at HF does not reconcile with Micrometals' formulas given for loss of #2 and #6 materials. Calculators that depend on those formulas are also wrong.
| Version | Date | Description |
| 1.01 | 31/05/2012 | Initial. |
| 1.02 | ||
| 1.03 | ||
| 1.04 | ||
| 1.05 |
© Copyright: Owen Duffy 1995, 2021. All rights reserved. Disclaimer.