ARRL transmission line loss graphs

The ARRL has for a very long time published tables and graphs of transmission line loss for common transmission lines.

ARRL nominal matched line loss graph

A widely accepted model for the loss in a transmission line at radio frequencies is that loss=k₁*f^0.5+k₂*f. In this expression, k₁ is a factor dependent on conductor losses which increase with the square root of frequency due to skin effect, and k₂ is a factor dependent on dielectric losses which tend to increase proportionately with frequency.

In most practical transmission lines (such as those in the ARRL graph above from the 20th edition of the Antenna Handbook), k₁*f^0.5 is much greater than k₂*f below 10MHz, and even up to 1GHz for many lines. Where k₁*f^0.5>>k₂*f, the slope of the lines in the graph can be found by calculus to be dominated by the first term, loss doubles for a fourfold increase in frequency. This means that one would expect that all lines in Fig 23 would be of the same slope at the left hand side of the graph, and it is obvious that they are not. This questions the accuracy of the graph.

Matched line loss from TLLC

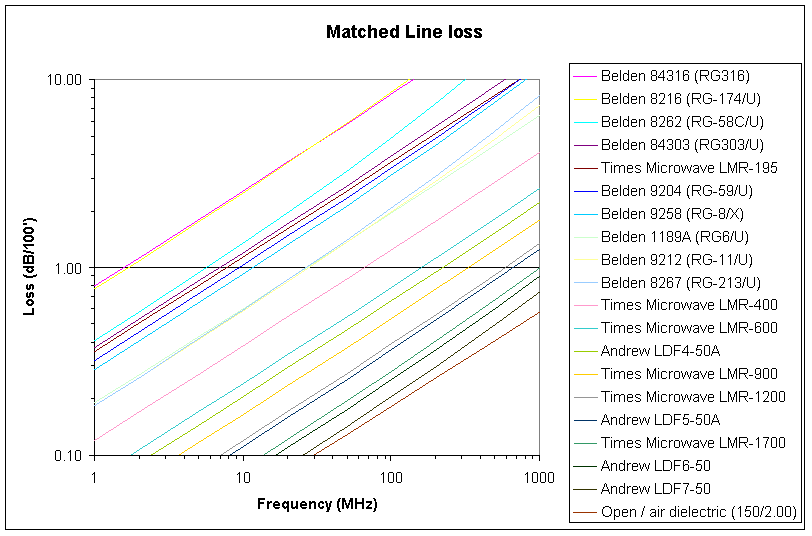
The graph above shows matched line loss for a range of common transmission lines using the coefficients from TLLC, calculated at frequencies of 1, 2, 5…1000MHz . It can easily be seen that the slope of all lines is approximately the same (as predicted above) below 10MHz, and at the higher frequencies, the effects of dielectric loss are manifest as an upwards sweep of the lines, more pronounced on some of the lines.

You will need to place a ruler against the graph to be sure your eyes aren’t playing tricks on you!

Note that the loss model used above assumes that skin effect is fully developed, and will not capture the effect of inadequate cladding of some CCS and SCS conductors at low HF frequencies.

The apparent errors in the ARRL’s graphs and underlying tables might explain why so many articles in its publications come up with some strange quantitative results when solving transmission line problems. The errors seem to also flow into some line loss calculators.