Category: Transmission lines

A simple transformer model of the Guanella 1:4 balun – some further observations

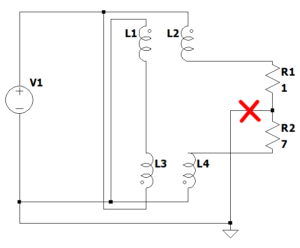
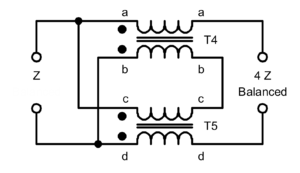
A simple transformer model of the Guanella 1:4 balun discussed a simple model for the operation of the device, but a model that is too simple for most RF baluns. Notwithstanding that, it does expose some interesting issues that are not only valid at lower frequencies, but will also be manifest in an RF balun.

Isolated load

Consider the effect of breaking the connection at the red X, so that we now have  what is often referred to as an “isolated load”. Continue reading A simple transformer model of the Guanella 1:4 balun – some further observations

Last update: 8th November, 2022, 4:50 AM

A simple transformer model of the Guanella 1:4 balun

(Guanella 1944) described a 1:4 balun, of a type often known as a current balun.

From Definition: Current Balun, Voltage Balun:

An ideal current balun delivers currents that are equal in magnitude and opposite in phase.

A good current balun will approach the ideal condition. It will deliver approximately equal currents with approximately opposite phase, irrespective of the load impedance (including symmetry).

Common mode current will be small.

If the load impedance is not symmetric, then the voltages at each output terminal will not be equal in magnitude and opposite in phase. (Note that for a truly ‘isolated’ load, one well represented as a two terminal load, the currents MUST be equal in magnitude and opposite in phase, but the voltages may not be equal in magnitude and opposite in phase.)

A simplified model

 

Above is a schematic of the Guanella 1:4 balun as often presented, this is an edited graphic from the ARRL manual, so may be familiar to readers. Continue reading A simple transformer model of the Guanella 1:4 balun

Last update: 7th November, 2022, 1:31 PM

Some wooly thinking on Antenna Factor online

Antenna Factor is often given / used as a parameter for an antenna (system).

An antenna with (nearly) constant AF can be quite convenient to simple field strength measurement where the AF value establishes a simple relationship between antenna terminal voltage and the external electric field strength.

Antenna Factor (AF) is the ratio of field strength to antenna terminal voltage for an antenna, dimensionally \({AF}=\frac{E}{V}=\frac{V/m}{V}=1/m\), AF units are 1/m or can be expressed in dB as \(AF_{dB}=20 \log_{10} AF \text{ dB/m}\).

It is lazy practice (though not uncommon) to simply express AF in dB, but wrong.  Continue reading Some wooly thinking on Antenna Factor online

Last update: 28th October, 2022, 8:29 AM

Diagnosis of a 9:1 transformer from NanoVNA plot – part 2

Diagnosis of a 9:1 transformer from NanoVNA plot discussed an example measurement of a 9:1 transformer on a binocular ferrite core. These are often recommended for use with Beverage antennas on 160 and 80m bands, and this was the maker’s application. In that article, I hinted that the core might not be #73 as the maker thought, or wished.

This article reports measurements of a 9:1 transformer wound on a Fair-rite 2873000202 (#73) binocular core. The pic above shows the test fixture. Continue reading Diagnosis of a 9:1 transformer from NanoVNA plot – part 2

Last update: 13th October, 2022, 8:23 AM

Diagnosis of a 9:1 transformer from NanoVNA plot

A chap recently posted online a question:

I have added two 1:9 transformer (2T/6T) back to back (high side together) and measured with the nanovna – 2 port measurement, as the binocular core I am not confident BN73 or not.

Also I swiped with one port S11, with one transformer where the high side is terminated with a 470ohm resistor load.

Please advise if it can be used for beverage antenna for 160/80m.

Let’s focus on the second test, and assume that the measurements are valid (and that is often an issue), that the 470Ω resistor is close enough to 450+j0Ω and the connections are short.

Above is his s11 sweep from 1 .5-7MHz.

I suspect this is actually #43 material. Continue reading Diagnosis of a 9:1 transformer from NanoVNA plot

Last update: 11th October, 2022, 4:26 PM

NanoVNA source mismatch error

One of the popular ideas online is that the correction process in the NanoVNA does not correct errors in mismatch at Port 1 and Port 2. This article deals with the first case ONLY, Port 1 mismatch.

An experiment with source VSWR nominally 2:1

A NanoVNA was configured with a SMA tee connected to Port 1 and a good 50Ω termination connected to the branch port, see the pic below. The left hand side of the tee becomes the new Port 1 interface, and by virtue of the additional 50Ω shunt termination, if the native Port 1 was indeed well represented by a Thevenin equivalent circuit with Zs close to 50+j0, the Thevenin source impedance is now closer to half that, Zs close to 25+j0.

Some would calculate this mismatch as causing a mismatch loss of 0.512dB that is additional loss in the s21 path.

Above is the test setup. The NanoVNA was SOLT calibrated with cal parts attached to the left hand side of the tee and the 200mm coax jumper from that point to Port 2. Continue reading NanoVNA source mismatch error

Last update: 6th July, 2022, 9:15 AM

NanoVNA-H – modification of v3.3 PCB to start the bootloader from the jog switch

Later NanoVNA-H* hardware allows the device to start in bootloader mode by holding the jog switch in whilst powering on. It is a very convenient facility for firmware update, much more convenient than taking the case apart to jumper BOOT0 to VDD. (Some later firmwares provide a menu option to start the bootloader… but of course that is only useful if the firmware is running properly and may not be useful in the event of a failed firmware update.)

This was a mod I devised prior to the v3.4 hardware change, it is not identical to that change as it preceded it, but it works fine on v3.3 hardware and may work on earlier versions.

Boot switch

The mod calls for replacing R5 with a 1k (1402) and running a short jumper from the T terminal of the jog switch to the un-grounded end of R6.

To use it, hold the jog switch in and turn the nanoVNA on.

Above a pic of the mod. It is a simple mod, but very fine soldering so it might not be within everyone’s capability.

Last update: 19th June, 2022, 7:40 AM

Digital display for Revex W560 directional wattmeter – part 1

The Revex W560 is a dual range VSWR meter that was also sold under other brand names.

W560-01

The low frequency range is specified as 1.8-160MHz.

This project is for an external digital display to suit the low frequency band of the W560. Whilst this project is for a specific meter, the techniques are applicable more widely. Continue reading Digital display for Revex W560 directional wattmeter – part 1

Last update: 15th June, 2022, 6:42 AM

How important is directional coupler Directivity?

How important is coupler Directivity?

Let’s discuss what the term means, and the uncertainty of measurement of DUT VSWR or ReturnLoss due to coupler Directivity.

Coupler performance parameters

 

Consider the above diagram, when terminated in a matched load, the key performance characteristics are: Continue reading How important is directional coupler Directivity?

Last update: 10th June, 2022, 7:23 AM