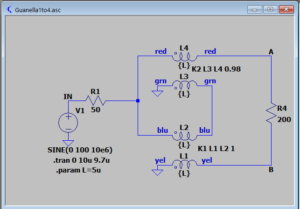
A simple two port VNA allows measurement of S parameters s11 and s21 of a DUT. Port 1 contains a directional coupler to transmit a signal into the DUT, and to capture and measure the amplitude and phase of the reflected wave relative to the forward wave at Port 1 (s11). Port 2 simply measures the amplitude and phase of the signal at its input, the forward wave after it has passed through the DUT relative to the forward wave at Port 1 (s21).
This is typically done by stepping (sweeping) the source on Port 1 through a range of frequencies, specified for example by start and end frequency and the number of discrete steps.
There are several source of error in such a measurement, but by making a series of measurements of some known configurations (Short, Open and Load on Port 1, Isolation and Through to Port 2), those errors can be determined and corrected out of subsequent measurements. So, there is a calibration process to measure and save measurements on these known loads, and then a correction process to apply the calculated corrections to raw measurements.
Early VNAs invalidated the calibration data if sweep parameters were changed, and so corrections were applied to raw measurements at corrections measured and calculated at exactly the same frequency.
This was really inconvenient, especially where no facility was provided to permanently save and restore a set of calibrations.
Later VNAs included the facility to interpolate (but not extrapolate) the calibration / correction data to a new set of sweep parameters. This was really convenient, but introduced a new source of error, the interpolation error.
When all this is done under the covers, users with little understanding of what is going on under the covers can easily obtain invalid / worthless results.
Let’s focus on s11 measurement, though the same issues exist for s21 measurement.
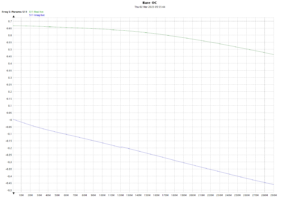
Above is a plot of uncorrected or raw s11 sweeping a NanoVNA-H4 101 points from 1 to 900MHz with nothing on Port 1 (approximately an open circuit OC). Ideally s11 should be 1+j0, but the directional coupler circuitry and small distance to the connector means the amplitude and phase vary as shown in the plot. Continue reading NanoVNA – interpolation – part 1
Last update: 17th March, 2023, 10:31 AM