This article describes a Simsmith model for an EFHW transformer using a popular design as an example.
This article models the transformer on a nominal load, being \(Z_l=n^ 2 50 \;Ω\). Real EFHW antennas operated at their fundamental resonance and harmonics are not that simple, so keep in mind that this level of design is but a pre-cursor to building a prototype and measurement and tuning with a real antenna.
The prototype transformer follows the very popular design of a 2:16 turns transformer with the 2t primary twisted over the lowest 2t of the secondary, and the winding distributed in the Reisert style cross over configuration.
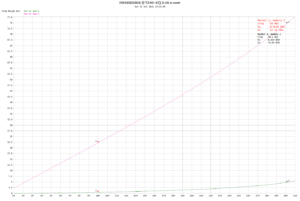
Above is a plot of the equivalent series impedance of the prototype transformer with short circuit secondary calculated from s11 measured with a nanoVNA from 1-31MHz. Note that it is almost entirely reactive, and the reactance is almost proportional to frequency suggesting close to a constant inductance. Continue reading A simple Simsmith model for exploration of a common EFHW transformer design – 2t:16t