The article Antennas – disturbing the thing being measured – open wire lines #5 demonstrated an inconsistency between the notion of a balun Common Mode Rejection Ratio CMRR property and a complete NEC model for predicting common mode current behavior.
In that case, two scenarios were modelled with only a change in the feed line length, yet they showed quite different currents near the same balun.
A common metric bandied around is the Common Mode Rejection Ratio (CMRR) and the definition is a bit rubbery, but it tends to come down to the ratio of the magnitude of common mode current to the magnitude of differential current in a test scenario (usually a lab workbench… with intention that the metric is then applicable more generally). (Anaren 2005) gives a popular explanation.
It is worth noting that the conventional meaning of CMRR in relation to op amps is that it is the ratio of differential gain to common mode gain and large +ve dB values are goodness, and it makes sense. Common use in terms of baluns is the opposite, Anaren gives the expression CMRR=S1c/S1d which will give large -ve dB values as goodness, and which seems inconsistent with the descriptive name where a large ratio (more +ve dB value) would be goodness. The balun ‘crowd’s’ use of a -ve rejection ratio seems a bit tautological, as if they haven’t really thought this through, it is a bit like the hammy thing of talking about the attenuation of a length of coax as -xdB.
I don’t think CMRR is a useful property of baluns per se, certainly not as a component of practical antenna systems, so I have written this article to report common mode ratio (CMR) (being the ratio of common mode to differential mode current at the point of interest). CMR is not a property of the balun, it expresses the relationship between the magnitudes of the components of current at a point of interest.
Keeping in mind that the differential current and common mode current distributions are usually both standing waves in the general case (usually with different phase wavelength and therefore relative phase), another dimension of the antenna problem is to look at the current distribution on the feedline of the NEC model scenario used for this series of articles. The model used here is the 20m feed line height and current balun with Zcm=1130+j1657Ω.
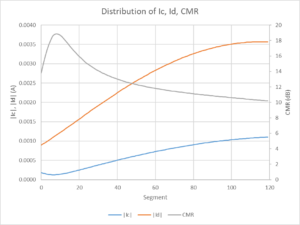
Above is a plot of |Ic|, |Id| and CMR in the NEC-4.2 model scenario. Segments are numbered from the lower end to upper end of the 20m long feed line. Continue reading Antennas – disturbing the thing being measured – open wire lines #6
Last update: 29th June, 2023, 9:05 AM





