At Where is the best place to measure feed point VSWR I discussed location of the VSWR meter and projection of its reading to another point on a known transmission line.
One of the conclusions drawn in that article is:
Feed point VSWR can be estimated from measurements made at another place if the transmission line parameters are known. It, like all measurements, is subject to error but it may be a manageable error and indeed possibly better overall than direct measurement.
This article discusses some issues that may arise in referring measurements from one place to another (eg near transmitter to antenna feed point).
Characteristics of transmission line categories
Let’s consider two categories of transmission lines in terms of characteristic impedance Zo and propagation constant γ:
- Lossless line; and
- practical line.
A lot of theoretical analysis uses lossless line for simple explanations, and whilst for a lot of purposes, approximation of practical line as lossless line serves well, at other times the error may be significant.
Lossless Line
A Lossless Line has imaginary part of Zo equal to zero and the real part of γ equal to zero.
Practical line
A practical line has non-zero imaginary part of Zo and non-zero real part of γ, and these are frequency dependent.
Under standing waves, attenuation along a practical line is not uniform, in most practical applications conductor loss/m is higher than dielectric loss so loss is higher near current maxima than near current minima.
For the purpose of this article, it is the frequency dependence of Zo, particularly the non-zero imaginary part that is significant.
A model
A model of a load similar to a 7MHz half wave dipole fed with 10m of RG58A/U was created in Simsmith to provide a basis for discussion. Whilst the model is subject to some errors computation, it is much less than comparing two field measurements at both ends of a transmission line.
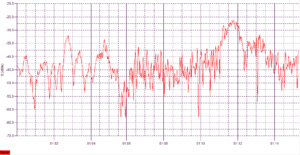
VSWR at each end of the transmission line
Let’s look at the ACTUAL VSWR. Actual means that if you were to observe the standing waves on the line (eg with a voltage probe), this is the VSWR you would expect to observe.
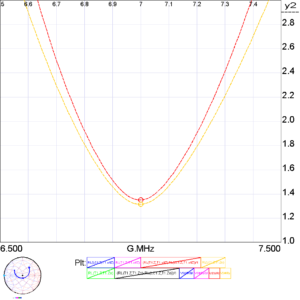
Firstly, observe that the source end VSWR (orange) is a little lower than the load end VSWR. This is by virtue of the attenuation on the line. The difference between the two can be calculated, but it is moderately complicated. Continue reading Where is the best place to measure feed point VSWR – error in Zo
Last update: 13th August, 2023, 6:52 PM