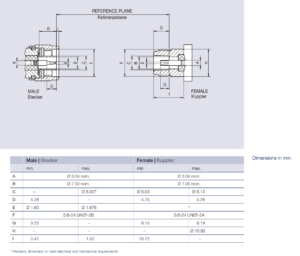
It has been my experience over more than 50 years that accurate measurements using SMA connectors requires that they be torqued to a consistent and adequate torque. Specifications for brass threads commonly runs around 0.6Nm, and I have a torque wrench calibrated for that torque which I use whenever the connectors are to be properly tightened.
In my NanoVNA-H v3.3, I reinforced the SMA connectors because of a sense that to tighten them to 0.6Nm (5.3inlb) caused the board to flex and over time might crack the tracks (Strength of reinforcement of nanoVNA-H connectors).
Joe Q Smith on NanoVNA SMA connectors
Joe Q Smith has an interesting video where he tests some Chinese SMA connectors to destruction, worth watching: NanoVNA Torquing SMA Connectors . In his tests, he needs upwards of 2Nm to damage the cheap Chinese end launch PCB connectors, more than three times the torque I use.
The new NanoVNA-H4
About 6 weeks ago, I took delivery of a new NanoVNA-H4, which as far as I can tell, is a ‘genuine’ Hugyen product.
I did not reinforce the connectors on my new NanoVNA-H4 because there was not the needed clearance for a similar adequate brass bar inside the case.
So, having used a torque wrench at 0.6Nm in the few weeks that I have owned the NanoVNA-H4, the connector on Port 1 failed.
Above, the failed connector has rotated, shearing two of the support pins and tearing the other two off the tracks. Continue reading NanoVNA-H4 v4.3 – broken SMA connector