Matching a quarter wave vertical using TL elements
A long time amateur friend dropped in the other day, and was interested in optimising his home brewed 10m mobile helical whip.
We measured the resonant frequency and feedpoint impedance using an MFJ259B. The indications were (and that is really all get from an MFJ259B) was that the antenna was resonant about 27.8MHz and had a feedpoint impedance of 50+j50 at 28.4MHz.
In view of his reluctance, no determination, to not modify the whip in any way, a transmission line solution looked the way to go.
This article generalises the problem to describe two simple ways to transform a quarter wave vertical to 50 ohms using common transmission line elements.
Example designs at 28.4MHz are given based on NEC modeling of a vertical over a perfect ground plane. Real antennas, especially verticals mounted on a motor vehicle will have impedances a little different to those shown here and so will require some adjustment to suit the actual load.
Both methods call for detuning the radiator to change to load impedance to one that can be transformed readily using common coax for the element(s). The methods are:
- to shorten the radiator element to increase the load impedance, until the resistive component of the parallel equivalent circuit is 50 ohms, then tuning out the capacitive reactance with a shunt short circuit stub; and
- to lengthening the radiator to increase the feedpoint impedance (R and X) significantly. The feedpoint impedance is then shunted with a s/c stub to further change the impedance to a point where the VSWR at 75 ohms is 1.5. A series 75 ohm line is then cut to length to transform that impedance to 50 ohms resistive.
Method 1
This method calls for shortening the radiator until the resistive component of the parallel equivalent circuit is 50 ohms, then tuning out the capacitive reactance with a shunt short circuit stub.
| Item | Value |
| Free space wavelength | 10.563m |
| Radiator length (m) | 2.365 |
| Radiator length (% of wavelength) | 22.4% |
| Radiator diameter | 0.02m |
| Z radiator | 30.5-j24.8 |
| Shunt s/c line Zo | 50 ohms |
| Shunt s/c line length | 51 deg |
This method is well known and has been described in various amateur handbooks.
I have used this method for an optimised match to an antenna for 2m where I had ready access to the underside of a centre roof mounted antenna and could plug a stub on to a socket soldered on the underside of the antenna base.
Method 2
This method calls for to lengthening the radiator to increase the feedpoint impedance (R and X) significantly. The feedpoint impedance is then shunted with a s/c stub to further change the impedance to a point where the VSWR at 75 ohms is 1.5. A series 75 ohm line is then cut to length to transform that impedance to 50 ohms resistive.
| Item | Value |
| Free space wavelength | 10.563m |
| Radiator length | 2.770 |
| Radiator length (% of wavelength) | 26.2% |
| Radiator diameter | 0.02m |
| Z radiator | 51+j45 |
The following is a Smith Chart solution. For clarity, the R and X circles have been omitted from the chart.
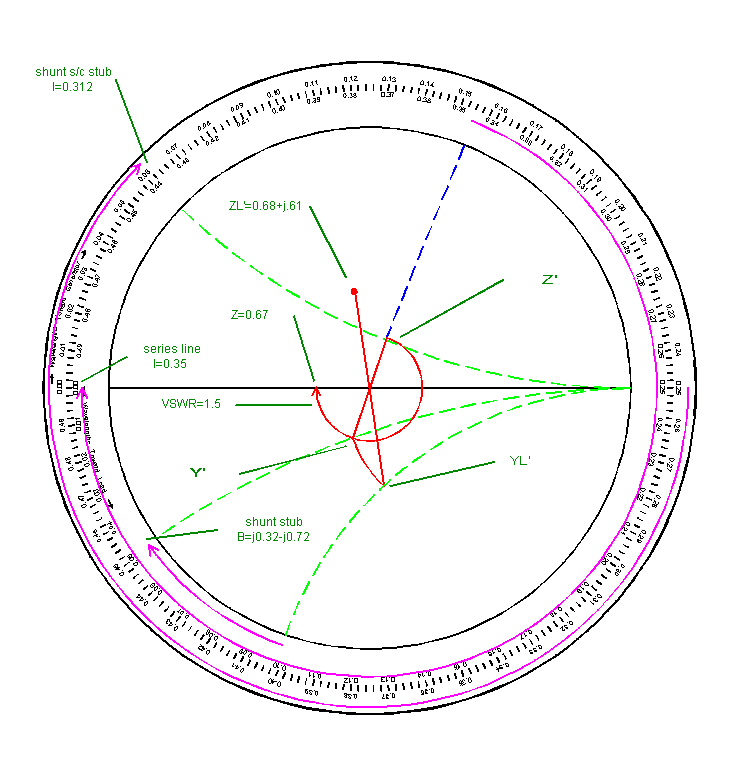 |
Solving on the Smith Chart
- plot the normalised ZL' (0.68+j0.61)
- convert to admittance (draw a diagonal to project the same distance the other side of the origin) and mark the point YL'
- draw in the VSWR=1.5 circle
- track along the constant conductance contour to intercept the VSWR=1.5 circle and mark the intercept point Y' (the objective is to excite a VSWR = 1.5 on the series line)
- calculate the difference in susceptance at 2 and 4 (it will be negative or capacitive) B=j0.32-j0.72 =-j0.4
- find the length of a s/c stub to deliver the capacitive susceptance by calculating the length in wavelengths clockwise from the infinite susceptance point to susceptance from step 5 (B=-j0.4, length of s/c 75 ohm stub=0.312 wavelengths or 112 degrees)
- convert the point from step 4 to impedance (draw a diagonal to project the same distance the other side of the origin) and mark the point Z'
- calculate the series line length tracking clockwise from the point marked in step 7 (Z') to the point where the normalised impedance is 0.67+j0 (50 ohms) (lengths of 75 ohm series line =0.35 wavelengths or 126 degrees).
| Item | Value |
| Shunt s/c line Zo | 75 ohms |
| Shunt s/c line electrical length | 112 deg |
| Series line Zo | 75 ohms |
| Series line electrical length | 126 deg |
To calculate the physical length, use the formula l= 3e8/f*vf*el/360 where f is the frequency and vf is the velocity factor for the line, and el is the electrical length in degrees. The series line could be extended by electrical half waves to repeat the 50 ohm impedance at a more convenient point, but the bandwidth is reduced with longer series line. Alternatively, the series line can then be extended with 50 ohm coax for any length.
Back to the mobile helical problem
Table 4 is the solution to the helical mobile whip.
| Item | Value |
| Resonant frequency | 27.8MHz |
| Radiator Z at 28.4MHz | 51+j44 ohms |
| Shunt s/c line Zo | 75 ohms |
| Shunt s/c line electrical length | 111 deg |
| Series line Zo | 75 ohms |
| Series line electrical length | 130 deg |