 |
| OwenDuffy.net |
|
| The wire in wire antennas is usually self supporting,
so must provide sufficient strength not only to accommodate
its own weight forces, but also wind forces which are usually much
greater. Additionally, wire elements may be required
to support additional loads such as insulators, feedlines, baluns etc.
A wire span needs sufficient sag to withstand the forces of high winds. |
Wire antennas are often rigged as a length of uniform wire between two fixed supports.
This article does not consider ice or snow loading, complex spans, or any form of concentrated additional loads.
A simple span is one where uniform wire is supported between two fixed supports at equal height, and there are no concentrated loads. The wire takes the form of a catenary. A catenary is the curve described by a hanging flexible chain or cable when supported at its ends and acted upon by a uniform gravitational force.
A shallow catenary can be approximated well by a parabola. Indeed, Galileo suggested that a chain hanging under gravity was a parabolic curve, but this was disproved in 1669 by Jungius. The mathematics of a parabola are much simpler than that for the catenary.
Sag of a wire span is the maximum vertical deflection of the span below the straight line between the supports.
Sag can often be measured quite conveniently by hanging a scale or sag board from each end of the span and sighting between the boards to measure the sag. Alternatively permanent marks at the desired sag can be made on each support using tape or paint for sightings. Specifying and measuring sag is a practical way of correctly rigging a span.
The sag of a parabolic span is given by the formula in Table 1.
|
Sag=(WS2)/(8T) |
|
| W | Weight force per unit length |
| S | Length of the span |
| T | Tension in the wire |
| Sag | The vertical deflection at span centre below the straight line between the supports. |
Example 1: Consider 1.6mm (#14 AWG) annealed copper used for a span of half of a half wave dipole on 80m, so the span is 20m. The Guaranteed Breaking Strength (GBS) of the wire is 241N, and allowing for a Safety Factor of 3.5 for standing rigging, the Working Load Limit (WLL) is 241/3.5 or 69N. The wire's weight force per metre (W) is 0.18N/m, so solving for Sag, Sag=(0.18*202)/(8*69) or 0.13m. If this span is rigged with LESS than 0.13m of sag, the tension in the wire under these load conditions will exceed its WLL.
Example 2: Consider the same data as in Example 1, but with combined weight and wind forces of 4.2N/m (wind speed 60m/s). Solving for Sag, Sag=(4.2*202)/(8*69) or 3.0m. If this span is rigged with LESS than 3.0m of sag, the tension in the wire under these load conditions will exceed its WLL. Note that with 3.0m of sag, the tension in the wire in the absence of wind loading would be just 5.3N or just 2.19% of GBS.
Example 3: Consider the same data as in Example 2, but using 1.6mm (#14 AWG) 30% Copperweld with combined weight and wind forces of 4.2N/m, and WLL 514N. Solving for Sag, Sag=(4.2*202)/(8*514) or 0.41m. If this span is rigged with LESS than 0.41m of sag, the tension in the wire under these load conditions will exceed its WLL. Note that with 0.41m of sag, the tension in the wire in the absence of wind loading would be just 20.7N or just 1.15% of GBS.
The wind speed used in Examples 2 and 3 is 60m/s (216km/h or 134miles/h) which is the AS4055 design wind speed for the worst case scenario in non-cyclonic parts of Australia. The Safety Factor use is 3.5 according to AS1418.5 Standing ropes, fixed guys.
Copperweld® wire (Copper-Clad Steel or CCS) is a composite in which a concentric copper cladding is metallurgically bonded to a steel core through a continuous, solid-cladding process using pressure rolling for primary bonding. The 30% designation means that it has 30% of the conductivity of copper wire of the same diameter, but for RF applications at HF, it will have close to 100% conductivity due to skin effect. MIG welding wire which is steel wire with a flash of copper is not to be confused with Copperweld.
Note that it is not the wire alone that determines whether a wire span will survive a given wind speed, a strong wire rigged with insufficient sag will operate at higher tension and may fail. A manufacturer that specifies a wind survival speed for an antenna but doesn't supply sag recommendations is fooling the buyer, they have not supplied sufficient information to enable compliant installation.
Popular conductors include Hard Drawn Copper, Copperweld, and Stainless Steel. Cadmium copper is used for higher strength, annealed copper has poor strength and is not suitable for more than the shortest spans, insulated annealed copper (eg building wire) is even worse having higher wind resistance (due to the insulation thickness) for its strength.
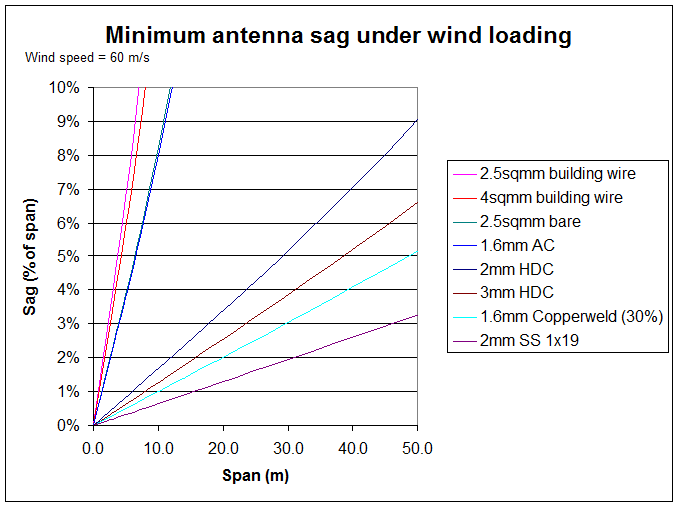
Figure 1 shows the minimum span sag under 60m/s wind loading for a selection of conductors that might be considered for a wire antenna. If the span is rigged in calm warm conditions with at least the minimum sag, the the sag under wind loading will be a little greater, depending on the elasticity of the conductor and give in the conductor supports. Most strong conductor materials will not stretch very much under the wind forces as the Young's modulus for the materials is usually very high. Allowance may need to be made in extremely cold environments for reduction in conductor length and sag at low temperatures.
 |
Figure 1 uses the more exact catenary equation rather than a parabolic approximation, so small differences may be observed between the chart and calculations using the parabolic formula.
A wire that requires more than 2% to 5% sag for a particular span is probably not suitable for the application, depending on the height of the span and the ability to accommodate a large amount of sag.
It can be seen from Figure 1 that annealed copper is not practical for longer spans, its strength is too low relative to its wind resistance and mass, even more so for insulated wires.
Figure 2 shows minimum sag for stronger wires over longer simple spans.
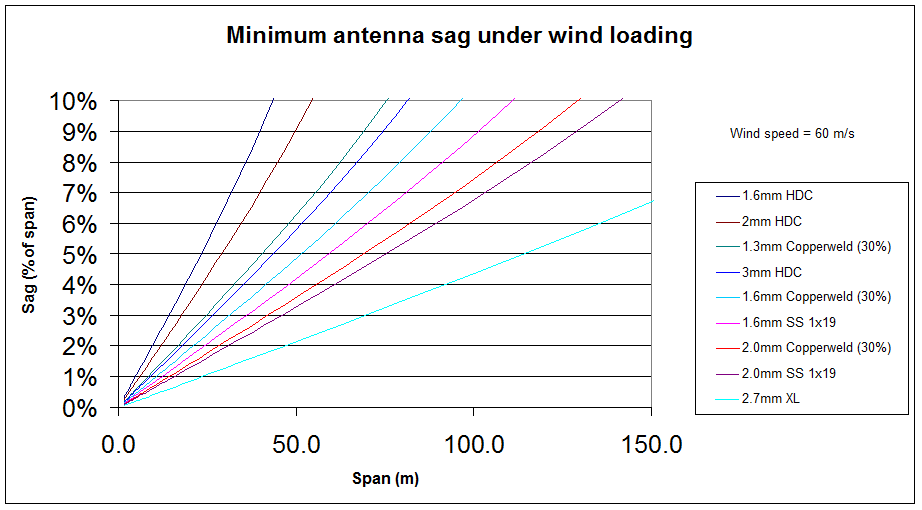 |
30% Copperweld has sufficient cladding thickness that the wire's conductivity is similar to copper over most of HF. Copperweld delivers most of the strength of medium/high tensile steel and the conductivity at HF of copper.
The 2.7mm dia "XL" wire is an electric fence wire by Gallagher. They claim it is a high tensile steel wire clad with aluminium, 30% by csa. Gallagher have supplied mechanical properties of the wire. The cladding thickness is 223 microns, which is sufficiently greater than the skin depth on HF that the wire's conductivity is similar to aluminium. XL delivers 70% of the strength of high tensile steel and the conductivity at HF of aluminium (about 78% of copper at HF due resistivity and skin effect).
Stainless steel has more loss than copper, and depending on the antenna, thin stainless steel wires may add 1 to 4 dB of loss compared to copper.
Small diameter stainless steel is used in many commercial wideband HF antennas. Many if not all of these antennas incorporate bulk resistive loss elements (eg T2FD designs) and loss in the antenna wire just means less loss needed in the bulk loss elements. If an antenna doesn't depend on inherent or built in loss to achieve objectives (such as improved VSWR over a wide frequency range), don't use stainless steel without considering its loss.
More complex configurations where for example, concentrated masses exist (eg feedline, balun), concentrated wind loads exist, or the supports are not at equal height, or the wire is not uniform are more complex to analyse, needing to be segmented into a series of simple spans with supports at appropriate heights at the connecting points and additional forces due to the relevant elements. There isn't really a typical "complex" scenario that is worth modelling to illustrate the effects. Suffice to say that adding concentrated loads to an existing wire will increase tension in the wire, and possibly exceed the WLL of the wire under the design load scenario.
Modelling complex spans is beyond the scope of this article.
Rules Of Thumb (ROT) that wires should be tensioned to 10% to 15% of GBS without wind loading do not provide for wind loading. Such a simple approach does not allow for the fact that for the same wire material, wind forces increase proportionally to wire diameter, while strength increases proportionally to the square of diameter. (Note that examples 2 and 3 above load the wire to just 2.19% and 1.15% of the GBS respectively in the absence of wind.)
The ARRL Antenna Handbook 18th edition has some information on sagging wire antenna spans on pages 20-2ff. Similar information may be in other editions.
There is no explicit discussion of wind loading, and the design guides (tables, nomographs, text) lead the reader to a design based on weight loading alone and with a Safety Factor of 10 or 5 depending on the chosen tension.
The approach in the ARRL Antenna Handbook 18th edition is NOT designed to withstand strong winds.
Antenna wire catenary calculator
| Term | Meaning |
| Breaking Force | see Guaranteed Breaking Strength |
| Breaking Load | see Guaranteed Breaking Strength |
| GBS | see Guaranteed Breaking Strength |
| Guaranteed Breaking Strength | The load or force stated by the rope manufacture as the rope's breaking strength when tested to failure in a new condition |
| Safe Working Load | The maximum load that may be applied under specific conditions of use to a crane, hoist, rope, chain, sling, or item of lifting gear |
| Safety Factor | The ratio of GBS to WLL |
| Sag | The maximum vertical deflection of the span below the straight line between the supports |
| SWL | See Safe Working Load |
| Ultimate Tensile Stress | The maximum amount of tensile stress that a component can be subjected to before failure |
| UTS | Ultimate Tensile Stress |
| WLL | See Working Load Limit |
| Working Load Limit | The maximum load that can be applied under general conditions of use to a crane, hoist, rope, chain, sling, or item of lifting gear |
| Version | Date | Description |
| 1.01 | 02/06/2006 | Initial. |
| 1.02 | 21/06/2006 | Fixed error in example 1 weight force. |
| 1.03 | 25/08/2006 | Added long span section. |
| 1.04 | 06/09/2006 | Updated XL characteristics with Gallagher's data. |
© Copyright: Owen Duffy 1995, 2021. All rights reserved. Disclaimer.