Wade's statistical nature of noise

A correspondent recently wrote to me pointing out the inconsistency with statements on the statistical nature of noise in some of my article and (Wade 1996) who states [t]he instantaneous noise voltage has a Gaussian distribution around the rms value, and asking me to explain / justify my position.

Johnson noise (white noise, thermal noise) can be thought of as a random process that gives rise to a time varying instantaneous charge due to random vibration of molecules, the higher the temperature, the greater energy involved in this process and the greater noise power available.

Though noise is a continuous process, we could quantise it and consider it a time series of instantaneous voltages and so long as the rate at which we quantise the noise phenomena is sufficiently high, the data capture will match that of any continuous instrument with equivalent bandwidth.

The quantisation process is akin to a statistical sampling process where a limited sample is drawn from a much larger population, in this case some thousands of instantaneous noise samples from a population being the continuous noise phenomena which has not start or end in a pure sense.

Fig 1:

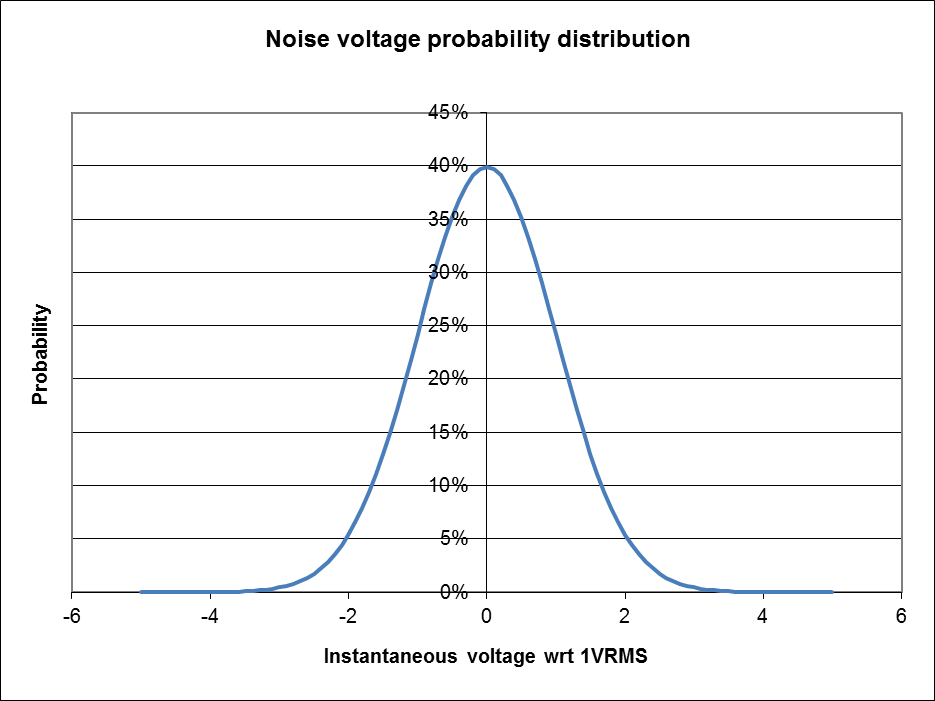
Fig 1 shows the probability distribution of instantaneous noise voltage of 1VRMS.

The noise process gives rise to instantaneous voltages that are normally distributed with a mean of zero and some variance. Having a mean of zero means it has zero DC component. It can be shown that the noise power available from a resistor is equal to the variance divided by the resistance, and it follows from that that the RMS voltage is equal to the square root of variance, or the standard deviation.

The fact that a pure noise process has a mean voltage of zero does not mean that a sample of the process has a mean of exactly zero, but it will have a mean that is very close to zero for a large sample size, and the probability that the mean is something else for a given standard deviation (RMS voltage) can be found using Student's T distribution. Effectively, the error of the mean of a measurement (or sampling) of noise that has a sufficient sample size to be useful will be insignificant.

(Wade 1996) states [t]he instantaneous noise voltage has a Gaussian distribution around the rms value.

Firstly, the normal distribution discussed above is a special case of a Gaussian distribution, the normal distribution is a more specific description of the distribution and not incompatible.

The words Gaussian distribution around suggest that the distribution has a central tendency to the RMS value. The central tendency of a normally distributed variable is the arithmetic mean (or just mean), and so with these words, Wade equates mean to the RMS value.

The ONLY case where the mean is equal to the RMS voltage is if v(t)=constant, ie it is a DC voltage and has no time varying component. That is incompatible with the description of noise as a time varying voltage, if the time varying component of a voltage is zero, there is no noise present..

I have raised this with Wade, and my feeling from his response (Paul Wade, 1/3/13 email message to author) is that he considers his original statement correct. Perhaps no one else has challenged it in the 17 years since he wrote the paper.

Changes

Version	Date	Description
1.01	05/03/2013	Initial.
1.02
1.03
1.04
1.05

Wade's statistical nature of noise

Links

Changes