This article documents a field strength survey of an M40-1 short helical vertical on 40m.
This test is more a feasibility study of the experimental method and apparatus than an absolute measure of the antenna.
The antenna under test is described at AUT – MobileOne M40-1 40m helical.
Field strength was measured using a small square untuned loop and VK3AQZ RF power meter (RFPM1), and data was captured using A prototype data logger for RFPM1.
Power meter
VK3AQZ RF power meter (RFPM1) described my build and calibration of the RFPM1.
 Above is the RFPM1, shown with two probes, but only one probe is required for this procedure, the other is disconnected. The RFPM1 directly reads input power in dBm.
Above is the RFPM1, shown with two probes, but only one probe is required for this procedure, the other is disconnected. The RFPM1 directly reads input power in dBm.
Loop antenna
The loop antenna used was described at (Duffy 2007). It is a small square loop (600mm sides) fed in one corner with a 1:1 voltage balun.
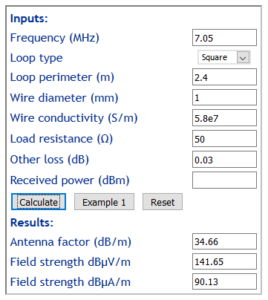
The important calibration constant is the Antenna Factor (AF) which is the ratio of the electric field strength to the voltage developed at the antenna terminals (loaded with 50+j0Ω).
Above is a calculation of the loop antenna factor (Calculate small loop Antenna Factor) used to convert measured voltage into field strength
Measurements
The test kit was walked at fairly constant speed from 20 to 60m from the antenna, to the side of the vehicle, and over a grassed clay paddock. Measurements were taken every 1s and distance interpolated over the set. Transmitter output power was measured at 40W, and feed line efficiency estimated at 90%.
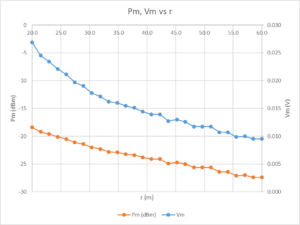
Above is a plot of the measured power and the calculated raw measured voltage.
Analysis
Initial
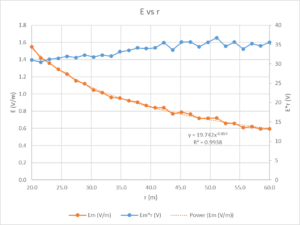
Above is the calculated E field strength after deducting ground loss using Norton’s ‘exact’ formula. Ground parameters are assumed to be σ=0.010, εr=4. Also shown is E*r.
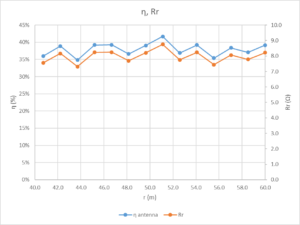
 Above is the calculated efficiency based on calculated cmf. Efficiency implies Radiation resistance (Rr).
Above is the calculated efficiency based on calculated cmf. Efficiency implies Radiation resistance (Rr).
The trendline for E departs from the expected inverse linear relationship, the exponent of the curve fit is 0.85 rather than 1.0, and begs the question of whether near field is significant in at least some of the measurements.
When less is more
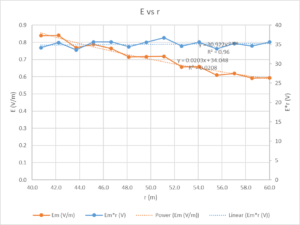
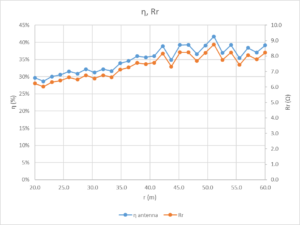
The following graphs consider only data for distance greater than 40m (approximately 1λ).
Above is the calculated E field strength after deducting ground loss using Norton’s ‘exact’ formula. Ground parameters are assumed to be σ=0.010, εr=4. Also shown is E*r.
A curve fit to the data has an exponent of -0.968, quite close to the expected value of -1.0 for E∝1/r.
Above is the calculated efficiency based on calculated E*r. Efficiency implies Radiation resistance (Rr). R^2 is poor because there are few data points and the slope is quite low.
Mean efficiency is 38.0% with a standard deviation of 1.9%. Keep in mind that this is not a full spatial survey, but a survey along one radial line from the antenna and it would be naive to assume antenna efficiency averaged over all azimuth directions is 38%.
Conclusions
- The method for interpolating distance does not seem to have introduced significant noise.
- Measurements in the more distant are closer to expected and suggest that closer measurements were affected by near field.
- Results are sensitive to ground parameters, more so G than ε, and to some extent, the test is a measure of ground parameters which clearly need to be assessed separately.
References / links
- Norton, KA. Dec 1941. The calculation of ground wave field intensity over a finite conducting spherical earth. Proc IRE, vol 29, pp 623-639.
- ———. Oct 1936. The propagation of radio waves over the surface of the earth and in the upper atmosphere Part I. Proc IRE, vol 24, pp 1367-1387.
- ———. Sep 1937. The propagation of radio waves over the surface of the earth and in the upper atmosphere Part II. Proc IRE, vol 25, pp 1203-1236.