| OwenDuffy.net |
|
Taking an example of an FT140-43 or Fairrite 5943002701 with 10 turns at 21MHz.
Inductance of an inductor wound on a high permeability core can be given as L=N2Al where Al=(µA)/(2πr) where N is the number of turns, A is the cross section area of the core, and r is the radius of the core, and µ is the permeability of the core. µ=µ0*µr where µ0=4πe-7 and µr is the relative permeability.
The impedance of an ideal inductor can be expressed as Z=jωL, or Z=j2πfL. Substituting for L, Z=j2πfN2Al.

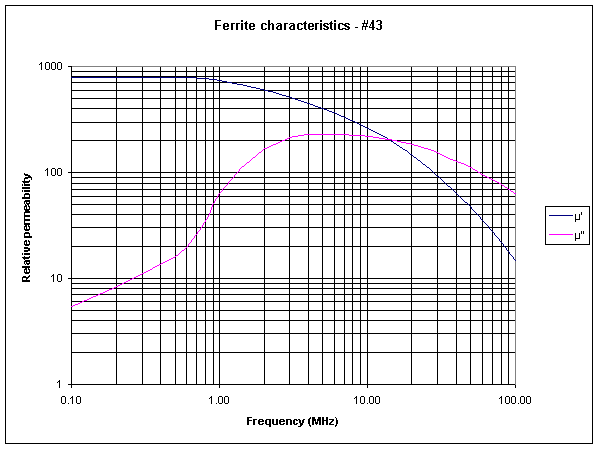
Relative permeability can be expressed as a complex quantity to capture both the ability of the core to increase flux and the core loss. The figure above taken from the data sheet gives µ’ and µ” over a range of frequencies.
The published data for the core gives Al=885e-9, but Al is based on the permeability at low frequencies (initial permeability, µi) where it is relatively constant, and must be adjusted for higher frequencies by multiplying by (µ’-jµ”)/µi.
So, we now have Z=j2πfN2Al(µ’-jµ”)/µi.
Let us put some numbers around that.
From the graph above, at 21MHz µ’=140 and µ”=180, and from the datasheet, µi=800.
Z=j2πfN2Al(µ’-jµ”)/µi.
Z=j2π21e6*102*885e-9(140-j180)/800=2627+j2044Ω. Note this is quite a different answer to calculation based on uncorrected Al, which suggests an inductance of 88µH and an impedance therefore of 0+j11680Ω.
It is also important to understand that a small amount of stray capacitance exists and it may significantly modify the inductor impedance.
If for example the inductor calculated to have Z=2627+j2044Ω is shunted with 2pF of stray capacitance, the impedance of the combination is given as 1/(1/(2627+j2044)+j2πf*2e-12)=3792-j1270Ω. Note that the effect of the stray capacitance is to make this inductor look like a high resistance with a series capacitive reactance… not what is perhaps expected of an inductor.
Some manufacturer publish graphs for specific cores of R and X for a single turn. These can be multiplied by turns squared, but the effects of stray capacitance need to then be factored in as above.
Beware of simplistic calculators and tools and techniques that take shortcuts that are not valid at radio frequencies.
© Copyright: Owen Duffy 1995, 2021. All rights reserved. Disclaimer.