 |
| OwenDuffy.net |
|
Guanella described several baluns and ununs in 1944 in his article entitled "New methods of impedance matching in radio frequency circuits".
One particular configuration, the 1:1 balun is of particular interest because of its popularity in various forms in antenna applications.
 |
Fig 1 is from Guanella's paper, and it shows his development of the transmission line model for the differential current path, and an inductor for the common mode current path.
This article proposes a lossy transmission line model of a practical Guanella 1:1 balun that is effective for all frequencies within and immediately adjacent to the pass band. The model is of a two wire or coaxial transmission line wound around a toroidal ferrite core, and includes:
Such a model can be used for exploring not only variations in design such as different core materials, wire thickness and spacing, number of turns, etc, but exploration of loads other than the nominally matched balanced load.
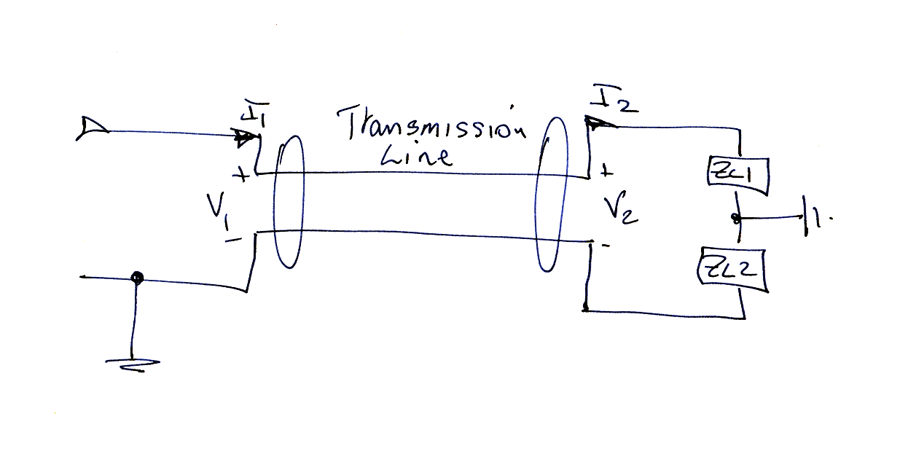 |
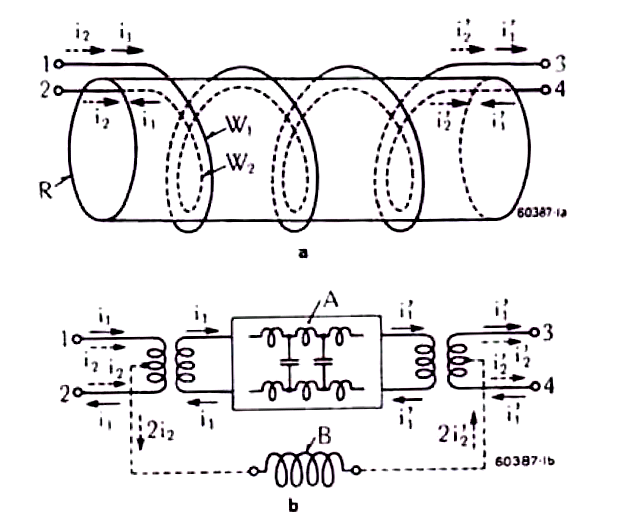
Fig 2 is a Guanella Order-1 Transmission Line Transformer configured as a common mode current choke. Note that the current designations are not related to Guanella's shown in Fig 1.
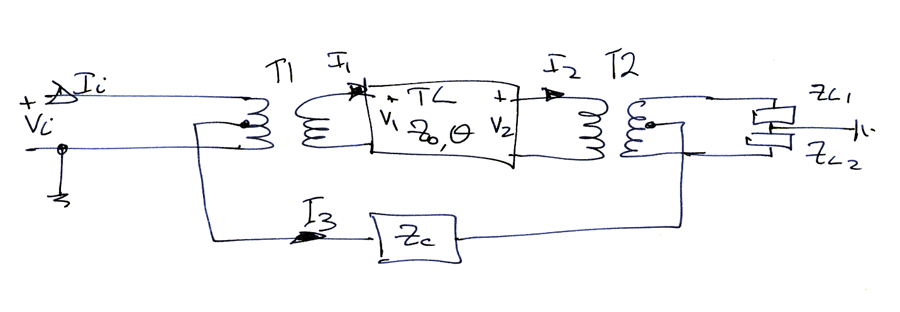 |
Fig 3 shows the proposed equivalent circuit. The transformers T1 and T2 are ideal transformers that are introduced for the purpose of separating the common mode and differential currents. The common mode current is routed through the common mode choke impedance Zc, and the differential current flows in the transmission line TL. The common mode current I3 is the result of components I3/2 which flow into both ends of the left hand winding of T1, and out of both ends of the right hand winding of T2. The differential mode current can be analysed by transmission line equations, and the common mode current can be analysed by lumped component circuit analysis.
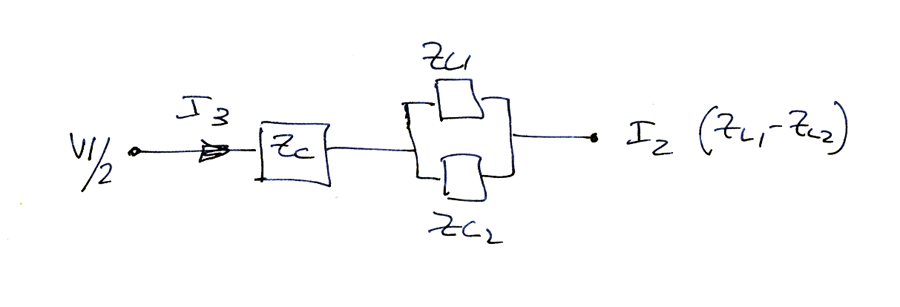 |
Fig 4 shows the I3 current path.
| \[V_1=V_2 cosh(\theta) + I_2Z_0sinh(\theta) \tag{1}\] \[I_2=\frac{V_2}{Z_l} \tag{2}\] Substituting (2) into (1)... \[V_1=V_2 cosh(\theta)+\frac{V_2}{Z_l}Z_0 sinh(\theta)\] \[\frac{V_1}{V_2}=cosh(\theta)+\frac{Z_0}{Z_l}Z_0 sinh(\theta)\] \[\frac{V_2}{V_1}=\frac1{cosh(\theta)+\frac{Z_0 sinh(\theta)}{Z_l}}\] |
Fig 5 is a solution to the proposed equivalent circuit. The quantity θ is the product of γ, the transmission line complex propagation coefficient, and transmission line length. All other currents, voltages, and powers can be derived from the V2/V1 relationship. Note that quantities in Fig 5 may be complex values, and many are frequency dependent.
Many models of this balun treat V2 as equal to V1, ie as if θ is zero, which is an approximation more valid at low frequencies.
The choke impedance depends on the ferrite core, and its ferrite permeability and loss are frequency dependent.
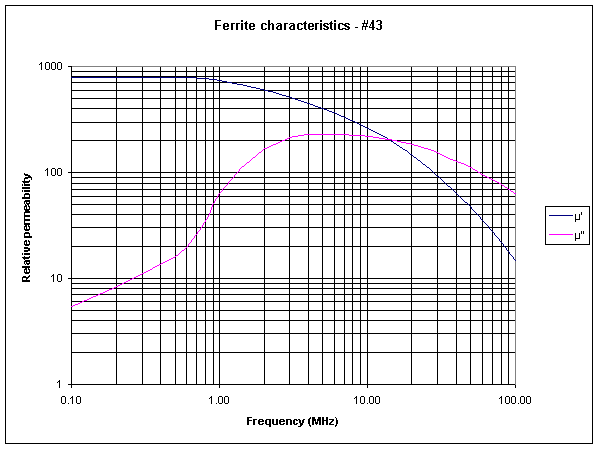 |
Fig 6 shows the characteristics of Fair-rite #43 mix. The choke impedance cannot simply be modelled as a fixed idealised inductor. The model needs to calculate the equivalent series inductive reactance and loss resistance at each frequency of interest. Choke impedance Zc=j*2*π*f*n^2*Al/µilf*(µ'-jµ'') where Al is inductance for 1 turn at µr=µilf, and µilf is the initial permeability at low frequency.
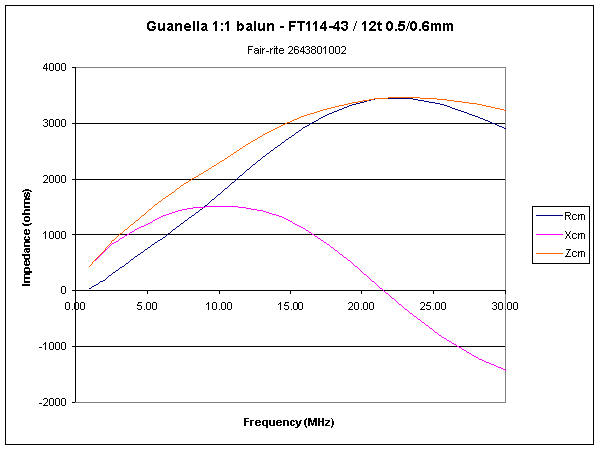 |
Fig 7 shows the impedance for a 12 turn choke wound on a Fair-rite 2643801002 (or 5943001001) #43 core (29mmx19mmx7.5mm) calculated from core dimensions and material characteristics and with a parallel capacitance of 1.6pF to calibrate the model to an actual choke. Quantity Zcm is the magnitude of Rcm+jXcm.
Measurement of a choke is likely to be more accurate than estimation from core dimensions, material characteristics and turns. Behaviour at high frequency is quite subject to stray capacitance.
Another challenge is that transmission line Zo and loss may be influenced by both skin and proximity effect. Skin effect causes the current to flow mainly on the surface of conductors, and proximity effect causes currents in opposite directions to tend to flow mainly on the adjacent surfaces of conductor that are very close together.
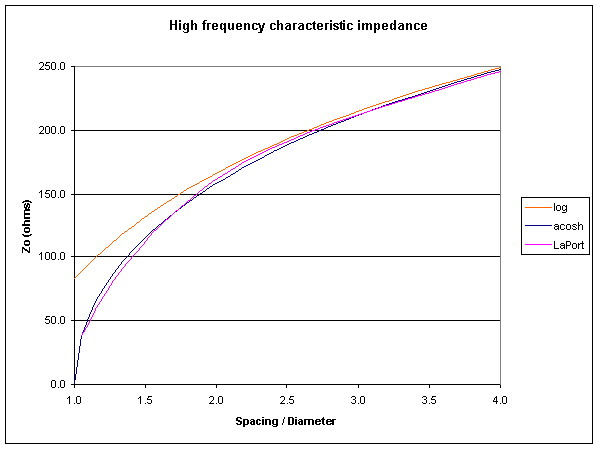 |
Fig 7 shows an estimate of Zo based on the log function, the acosh function, and a proximity corrected curve derived from Fig 4.23 of Radio Antenna Engineering by Edmund LaPort, 1952. It would appear that LaPort's graph may be a correction to the log function that he gives in the book, and an estimate of the cosh curve. Neither appear to properly account for proximity effect on Zo. Chipman (Transmission Lines) suggests that the error in Zo due to proximity effect is small for D/d>2 (Zo<160Ω). The acosh curve underestimates Zo for D/d<2 and the error may become significant.
A proximity resistance correction is calculated using an algorithm from the program line_zin.pas by Reg Edwards (G4FGQ).
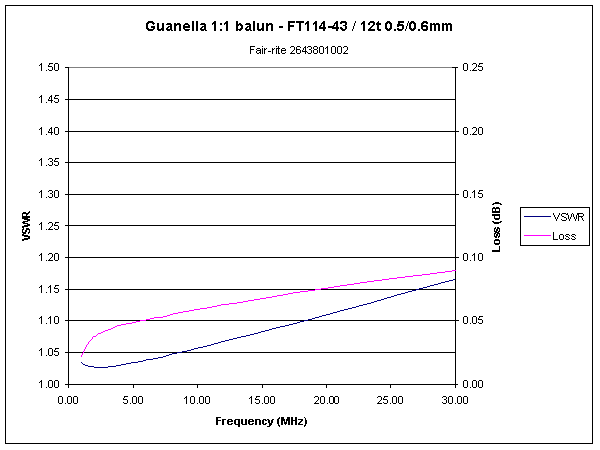 |
Fig 8 shows a plot of VSWR and loss modelled for a Guanella 1:1 balun made with 12 turns of transmission line wound on a Fair-rite 2643801002 (or 5943001001) #43 core (29mmx19mmx7.5mm). The transmission line comprises 0.5mm diameter copper conductors spaced 0.6mm centre to centre. Under matched conditions, losses are very low, 2% at worst. Estimating that the core can probably safely dissipate up to 5W, the balun is probably capable of continuous power rating of 250W.
Fig 7 shows common mode impedance. Common mode impedance is medium to high, which means that this type of balun does offer significant impedance to common mode current, eg on an antenna feed line connected to the balanced port.
Conclusions are:
| Version | Date | Description |
| 1.01 | 08/02/2008 | Initial. |
| 1.02 | 07/03/2008 | Added stray capacitance to model. |
| 1.03 | 04/04/2008 | Typo in Fig 5 corrected. |
| 1.04 | ||
| 1.05 |
© Copyright: Owen Duffy 1995, 2021. All rights reserved. Disclaimer.