 |
| OwenDuffy.net |
|
QEX published an article entitled "Coaxial Traps for Multiband Antennas, the True Equivalent Circuit" by Karl-Otto Muller (DG1MFT) in Nov/Dec 2004. This article is a comment on that article.
 |
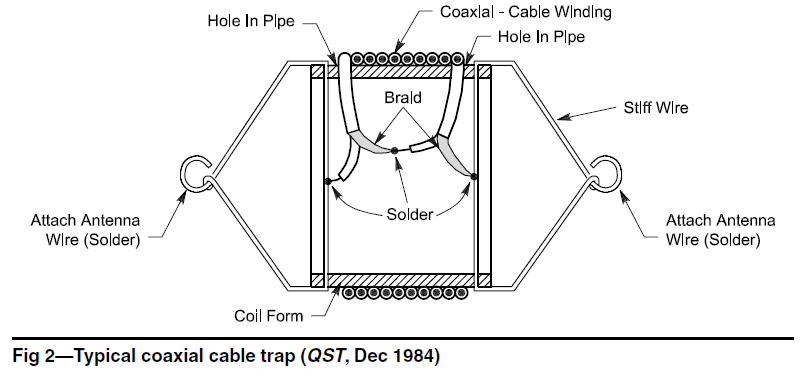
In his article "Coaxial Traps for Multiband Antennas, the True Equivalent Circuit", Muller states "As shown in Fig 2 (shown above), the inner conductor of the coil end is connected to the outer conductor at the beginning. Therefore the current is going around the core two times the number of turns." This suggests that the current in each pass through the structure (once on the inner conductor and once on the shield) gives rise to external magnetic flux that define's the structures inductance, and that the inductance of the coil is four times that which might be expected of a solenoid of those dimensions and the same number of turns as turns of coax.
The explanation that current "is going around two times the number of turns" suggests that the current on the inner conductor creates magnetic flux that links the outer conductor and vice versa. If skin effect is fully effective, this does not happen as the field due to current on the inner conductor is fully contained withing the coax dielectric space.
 |
Above is a magnified view of the coil ends from Muller's FIg 6.
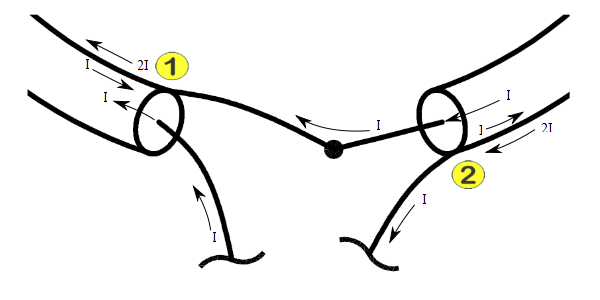
Let us consider the current flows where:
Assumptions 1 and 2 mean that the current is uniform in amplitude and phase at all points along the conductors.
Assumption 3 means that current flows only in the surface region of the conductors and current on the inside surface of the shield is effectively isolated from current flowing on the outside surface of the shield, as if there was a thin insulating layer between those surfaces.
TEM propagation in a coaxial cable means that if a current flows on the outer surface of the inner conductor, there is an equal current flowing on the inner surface of the outer conductor in the opposite direction.
Let us designate a current I flowing from the LHS terminal into the LHS inner conductor. That has two immediate consequences:
As a consequence of 2 above, there is:
By Kirchoff's Current Law, node 1 has I flowing into it from the LHS inner surface of the outer conductor and I flowing into it from the RHS inner conductor, so 2I must flow away from node 1 on the outer surface of the outer conductor.
So, 2I must flow around the outer surface of the outer conductor and into node 2. Since there is current I flowing from node 2 into the RHS inner surface of the outer conductor, there must be current I flow downwards from node 2 to the RHS terminal.
So, for terminal current I, there is current 2I flowing on the outer surface of the outer conductor around the loop. Any implication that current on the inner conductor contributes directly to external flux is conceptually wrong. In TEM mode, the magnetising force due to the return current on the inside of the outer conductor cancels the magnetising force due to the current on the inner conductor and there is no external flux due to those currents.
VE6YP's calculator (mentioned in the original article) does give a reasonably accurate estimate of the inductance of the solenoid formed by the outer conductor. Muller's inability to reconcile his measurement of the bootstrapped coil is due the the inherent 4:1 impedance transformation at low frequencies. (This is not to recommend VE6YP's calculator, like Muller, he fails to recognise the coax is a transmission line and not well represented as simply a capacitance proportional to length.)
Muller and VE6YP both treat the coax as an equivalent capacitance directly proportional to its length.
It is true that a very short length of very low loss coax has an impedance that is almost purely capactive and proportional to length.
Where those assumptions apply, the coax can be approximated reasonably as a capacitance which can be calculated from coax datasheets.
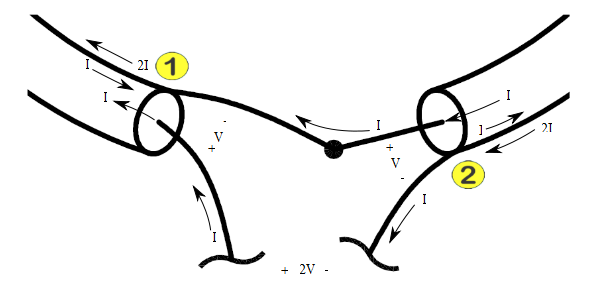 |
Fig 3 shows the voltages within the coax trap. Note that the equivalent capacitance appears in shunt with the inductance of the coiled coax shield and both the inductance and capacitance are subject to a voltage of half the terminal voltage of the trap.
Because the 1:2 current transformation, there is a 4:1 impedance transformation of (L//C), the terminal impedance behaves as though it is 4L in parallel with C/4 where L is the inductance of the coiled coax shield, and C is the capacitance of the coax.
The foregoing model is premised on the assumptions:
The problem is that these assumptions do not usually hold true in the region of the first trap resonance, much less at higher frequencies that might be relevant in a multi band antenna.
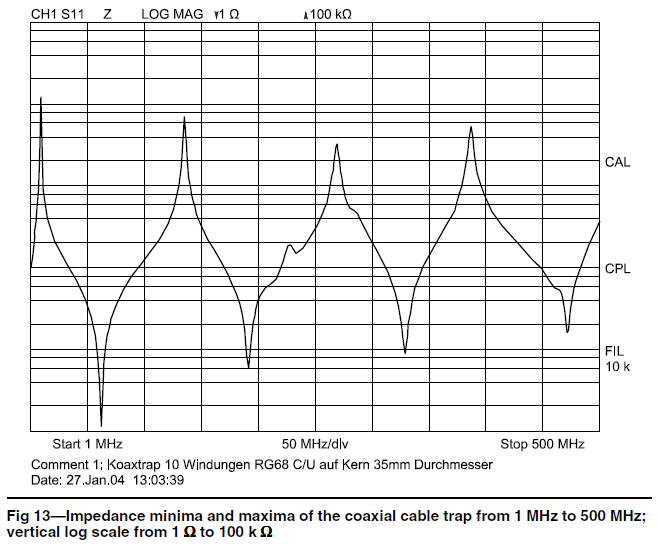 |
Fig 4 shows Muller's measurements which demonstrate that the trap cannot simply be represented by an equivalent circuit of 4L // C/4. The simplified circuit would give only one impedance peak at approximately the same frequency as the first peak in Fig 4, but would not predict any minima or other maxima.
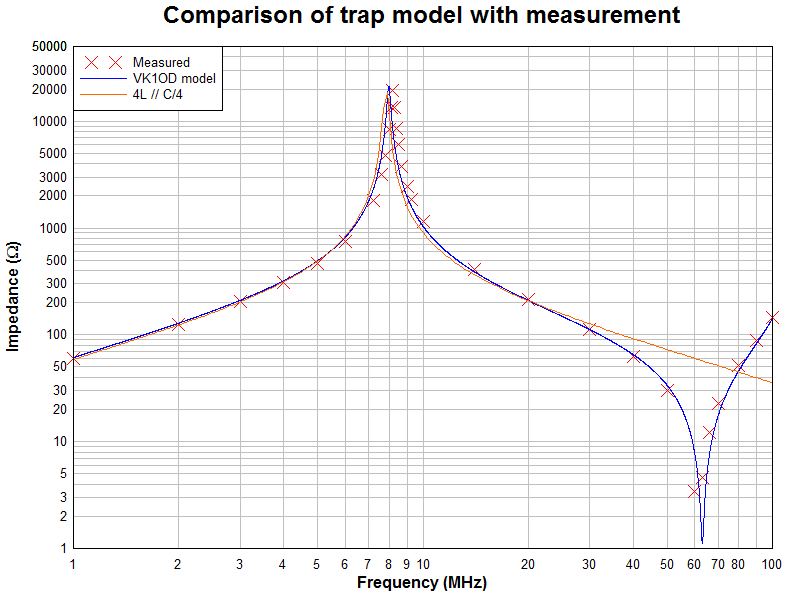 |
Fig 5 compares shows Muller's measurements, the VK1OD trap model, and the 4L // C/4 model which again demonstrates that the trap cannot simply be represented by an equivalent circuit of 4L // C/4.
The impedance values obtained from the 4L // C/4 have significant error in the region of resonance and at all higher frequencies.
The 4L // C/4 is not a "True Equivalent Circuit" as claimed.
| Version | Date | Description |
| 1.01 | 02/04/2011 | Initial |
| 1.02 | ||
| 1.03 | ||
| 1.04 | ||
| 1.05 |
© Copyright: Owen Duffy 1995, 2021. All rights reserved. Disclaimer.