 |
| OwenDuffy.net |
|
This article presents a theoretical and model based exploration of the G4CQM 50ohm coaxial dipole (PowAbeam 2011), which is a feed element for a VHF Yagi.
PowAbeam Antennas say (PowAbeam 2011) ...
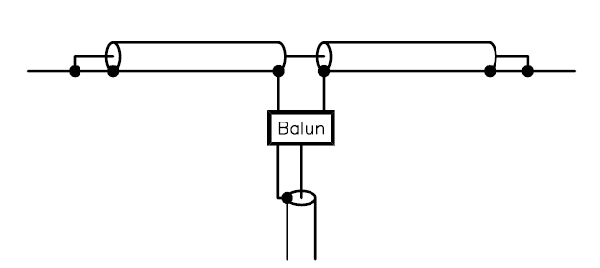
The G4CQM COAXIAL DIPOLE is essentially formed from two 1/4 wave shorted end stubs. By connecting the inner conductors together at its centre and creating one complete length of inner conductor, forces the outer conductors of the dipole (the radiating elements) into being equal, i.e. having the current node at the dipoles centre and equal voltage nodes at its tips as with any split dipole fed from a balanced source! However, there is NO current flow at the centre of the inner conductor.
Fig 1: G4CQM 50Ω coaxial dipole Content removed...
Because the inner conductor is electrically longer than it should be, terminating at the dipole ends and not part way down accounting for Vf, it lowers the Q of the dipole and increases bandwidth as seen in the VNA plot below....
And later:
THE BOTTOM LINE WITH G4CQM's COAXIAL DIPOLE: NO MATCHING, NO TUNING, NO PIPE BENDING, NO (DUBIOUS & LOSSY) BALUNS, NO MESSY COILS OF COAX, NO LOW IMPEDANCE, NO HIDDEN LOSSES AND NO COMPROMISE!
The structure looks somewhat familiar in concept and the word explanation is not at all clear.
 |
Readers will note the similarity in the structure between the well known Double Bazooka in Fig 2 (from ARRL) and the G4CQM 50Ω coaxial dipole in Fig 1 (from PowAbeam Antennas). The difference is about the physical and electrical lengths of the two coaxial stubs that appear each in series, then in parallel with the feed point. The operation is discussed in more detail at Double Bazooka Antenna performance (Duffy 2007).
In a Double Bazooka, the dipole would usually be a half wave from end to end, and the coax sections would be an electrical quarter wave each so shorter as shown if the dielectric constant is greater than one.
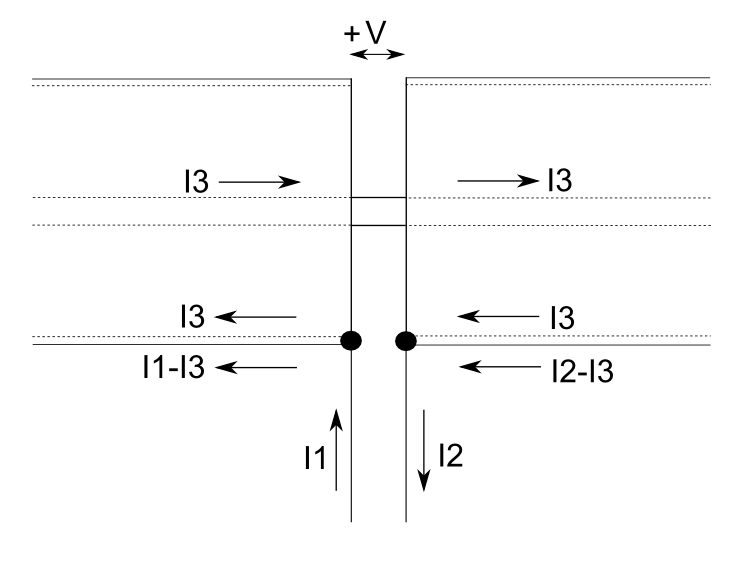 |
Fig 3 shows the currents at the feed point on the feed line, outer surfaces of the elements, inner surfaces of the elements, and outer surface of the inner wire taking I1 and I2 to be feed line currents, and I3 to be the current on the inner wire.
There is nothing in this system of currents that constrains or coerces I1 to
equal I2, I2 is in not way locked to I1 because of the dipole, with or without
the stubs. Though in this isolated circuit, it might appear that I1 must equal
I2, in a real antenna application where symmetry is compromised (eg by a coaxial
feed line), nothing in this driven element structure discourages common mode
current. It is an error in thinking to assert that there is some integral balun function that would tend to make I2 equal to I1. The claim of NO
(DUBIOUS & LOSSY) BALUNS
(required) is wrong, the explanation that By
connecting the inner conductors together at its centre and creating one complete
length of inner conductor, forces the outer conductors of the dipole (the
radiating elements) into being equal...
is wrong.
A dipole in free space with an infinitesimal source at its centre is intrinsically balanced, but dipoles in the real world usually require additional measures for good balance, especially when fed with coaxial transmission line.
Hilleard cites (PA0SIM Mar 2007) as authority that a folded dipole is a 'self balancing antenna' and hence that the G4CQM dipole is a 'self balancing antenna'. (PA0SIM Mar 2007) gives no explanation for his claims other than a graphic of a poor NEC model (folded dipole with common mode conductor terminated in an open circuit, and the dipole is fed with an unbalanced off centre source. (Duffy 2010) explores dipoles with a range of feed arrangements, and demonstrates that some feed line lengths and terminations act as an integral balun device. In fact, the principles are well known and are employed on some VHF and UHF antenna designs. It is true that a half wave folded dipole tends to drive less common mode feed line current than a plain half wave dipole by virtue of their coupling, but the G4CQM is not a folded dipole with coupled parallel conductors (the fields inside the coaxial elements do not interact with the fields due to the current on the outer surface).
The benefits of using an effective balun are quite the same as those that accrue if the antenna used an ordinary centre fed dipole.
There is nothing new about the Bazooka concept. Some key points:
The discussion about the location of voltage nodes and current nodes is unsupported and unconventional. If the centre feed point is 50Ω, the the centre of the dipole is NOT a current node, it is like any ordinary half wave dipole, a current antinode (ie maximum). This means that if the dipole is approximately a half wavelength from end to end, the ends are at or close to a voltage antinode (ie maximum). The discussion shows a basic lack of understanding of how the stub works, and or the ability to decompose the device into simpler underlying elements.
At http://g4cqm.www.idnet.com/2M%20YAGI/images/demoulding.jpg (Hilleard 1999), is a drawing of the dipole structure. It would appear to be a pair of 16mm OD tubes, with a piece of RG58 centre conductor with dielectric lying loose in the invert of the tube, and riveted to the outside ends of the tubes.
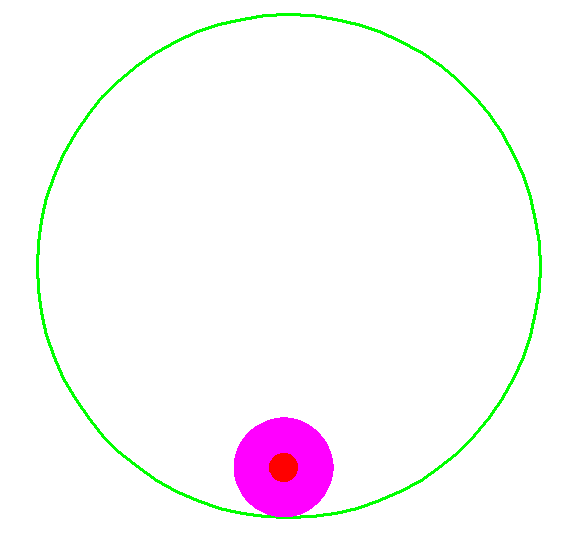 |
An ATLC model (Fig 4) of that structure suggests that Zo is 76Ω, and vf is 71%. Note that the inner conductor does not appear to be fixed in place, and the variation at the end with sealant and termination means that this estimate is only approximate as the line is not uniform. Further, these assumptions might not be valid for a vertically oriented dipole.
So, in the G4CQM 50Ω coaxial dipole, the full length stubs are clearly not 1/4 wave shorted end stubs
, but greater than 0.3λ.
If indeed there is NO current flow at the centre of the inner conductor
then it can be removed without affecting operation. It is the current flow into
the stubs that delivers the partial reactance compensation that gives the
bandwidth extension, and whilst there might be almost zero current at the
quarter wave resonance of the stubs, it is not true to say there is NO current flow at the centre of the inner conductor
.
If the series stubs were lossless, then current I3 in Fig 3 would be given by I3=V/(j*2*Zo*tan(l*/vf*f/299792458*2*π)) where Zo is characteristic impedance of the stub, l is the length of each stub, vf is velocity factor of the stub, f is frequency.(For the scenario for Fig 7 below, I3 would be about -j0.25A at 100W.)
To evaluate the effect of the driven element in a scenario that would result in an ordinary centre fed dipole having a feed point impedance of close to 50+j0Ω, a series of NEC models was built of a 'formula design' DL6WU 10 element Yagi for 144MHz using DL6WU Long boom Yagi design tool. To give the most valid results, the formula design was optimised by adjusting the position and length of the driven element to achieve feed point impedance of closer to 50+j0Ω, achieving VSWR < 1.02. The DE length is 481mm a side, position is 384mm from the reflector.
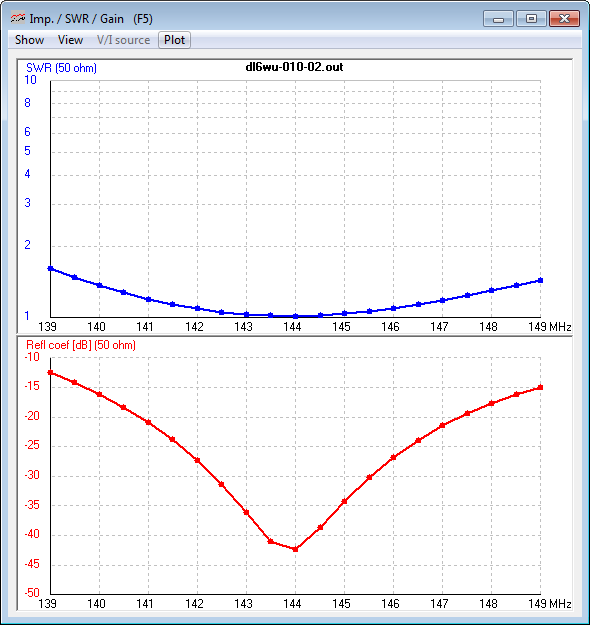 |
Fig 5 shows the VSWR and |ReflectionCoefficient| of the optimised 'formula design' DL6WU using a 16mm OD centre fed dipole of 496mm a side.
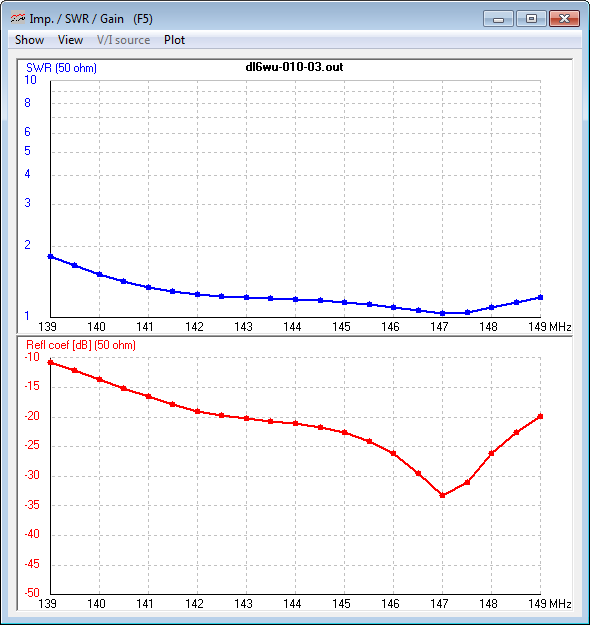 |
Fig 6 shows the VSWR and |ReflectionCoefficient| of the optimised 'formula design' DL6WU using a 16mm OD centre fed dipole of 481mm a side with lossless G4CQM stubs. As would be expected, the capacitive stubs have raised the point of minimum VSWR.
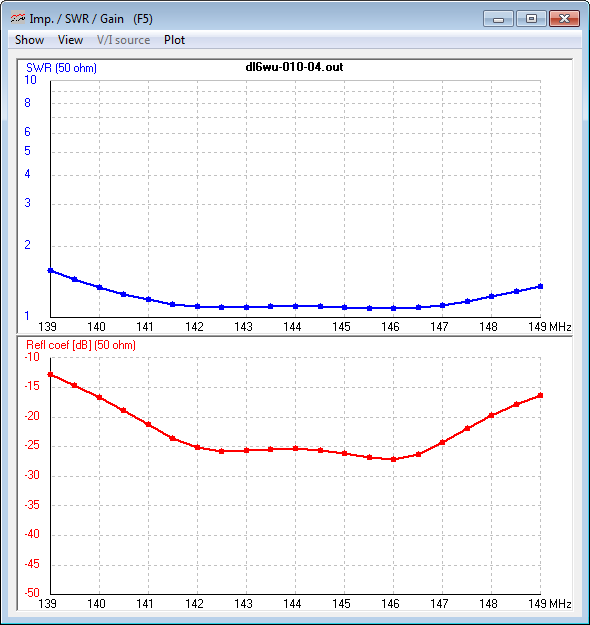 |
Fig 7 shows the VSWR and |ReflectionCoefficient| of the optimised 'formula design' DL6WU using a 16mm OD centre fed dipole of 486mm a side with lossless G4CQM stubs. The DE length is a result of retuning to shift the point of minimum VSWR back to 144DE length is a result of retuning to shift the point of minimum VSWR back to 144MHz
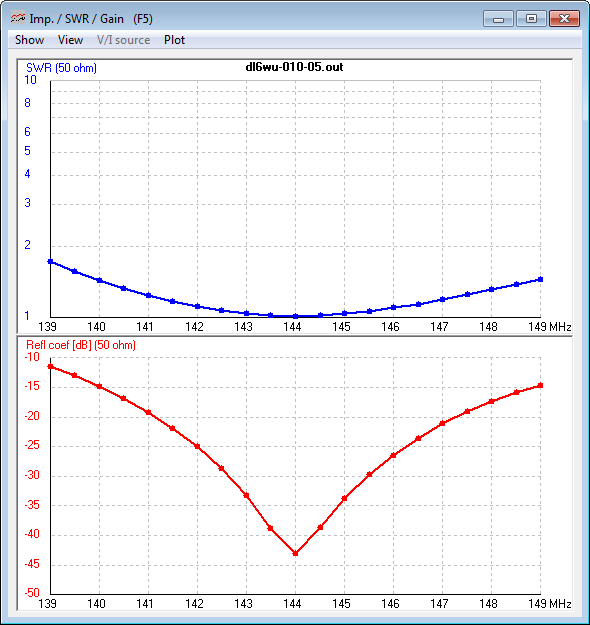 |
Fig 8 shows the VSWR and |ReflectionCoefficient| of the 'formula design' DL6WU using a 16mm OD centre fed dipole with lossless G4CQM stubs. The formula design with stubs was optimised by adjusting the position and length of the driven element to achieve feed point impedance of closer to 50+j0Ω, achieving VSWR < 1.02. optimised for minimum. The DE length is 486mm a side, position is 366mm from the reflector.
It is a relatively easy task to compare the VSWR bandwidth of Fig 5 and Fig 8 given a VSWR criteria, the thing is that you will get different answers depending on the choice of critical VSWR. There is not a practical difference between the curves. (The difference in minimum return loss is not significant, it is an accident of optimisation, and both configurations could be improved by further running of the optimiser.)
Without quantifying the additional loss of the stub sections, it is not possible for any person to make a rational judgment as to whether the achieved bandwidth extension is worth the cost in their situation, but the loss in such a short stub is likely to be fairly low.
PowAbeam Antennas claims bandwidth improvement but without making an quantitative comparison with an ordinary dipole as a driven element in any specific Yagi.
None of this is to suggest that PowAbeam antennas might not work well, but the claims and PowAbeam explanation of this not-so-novel driven element discussed above are not born out in the models above.
| Version | Date | Description |
| 1.01 | 02/09/2011 | Initial. |
| 1.02 | 05/09/11 | ATLC, NEC models added. |
| 1.03 | 07/09/11 | Optimised NEC models added. |
| 1.04 | ||
| 1.05 |
© Copyright: Owen Duffy 1995, 2021. All rights reserved. Disclaimer.