Amateur Radio application of Frequency Modulation

This article explains the theory of Frequency Modulation (FM), methods of producing FM, applications, and test and measurement techniques, with a practical emphasis on Amateur Radio applications.

It was written to improve the understanding of this mode by Radio Amateurs.

Overview

Fig 1: FM wave (greatly exaggerated).

Frequency modulation (FM) is widely applied in Amateur Radio for voice, telegraphy and data modulation. This article gives an overview of the theory of FM, its application, and applied test and measurement techniques.

We use the term Frequency Modulation fairly loosely, more generically we are usually talking about a form of angular modulation, and most often, narrowband voice communications signals are actually Phase Modulated (irrespective of whether they were created with a phase modulator or a frequency modulator). Confused? Read on!

The article explains the theory of FM and should convince you that FM is not so difficult to measure. Indeed with an audio signal generator with known frequency calibration, an audio milli-voltmeter or oscilloscope, and an SSB receiver it is relatively easy to calibrate an FM modulator and transfer the calibration to a demodulator. There is even a link to an audio demonstration of the technique.

Definitions

Amplitude Modulation (AM) is a system where the frequency of a carrier wave is held constant while the amplitude is varied in sympathy with the voltage of the modulating signal.

Frequency Modulation (FM) is a system where the amplitude of a carrier wave is held constant while the frequency is varied in sympathy with the voltage of the modulating signal.

Phase Modulation (PM) is a similar system where the phase of the carrier wave is varied in sympathy with the voltage of the modulating signal, and as in frequency modulation, the amplitude of a carrier is held constant.

Angular Velocity is the rate of change of phase (usually expressed in radians per second).

The Radian is a unit of angular displacement (as is degrees), there are 2 * pi radians in a full circle (or 360°), so a radian is approximately 57°.

Frequency is a measure of the number of repetitions of a periodic waveform in unit time (1 second). Frequency of a carrier wave is related to Angular Velocity, there are 2 * pi radians in each cycle of a carrier wave, so the Angular Velocity is 2 * pi * frequency.

Pi is a numeric constant, it's value is approximately 3.141592654. (You can approximate it by using 22/7 - the error is less than 0.05%).

Theory of frequency and phase modulation

Frequency or Phase - what is the difference

There are two general types of modulation of a carrier wave, Amplitude Modulation and Angular Modulation. Frequency and Phase Modulation are related, they are different forms of Angular Modulation, although you won't hear that term in general use.

Now Phase and Frequency are related, an incremental frequency shift of the carrier wave frequency causes a continuing change in phase (wrt the original carrier), the rate of change of phase is proportional to the frequency shift. Angular Velocity is the rate of change of phase. Frequency is the Angular Velocity divided by 2 * pi.

Alternatively, you can consider that to change the phase of the carrier, the frequency had to shift for a period, the phase change is proportional to the integral of the frequency shift over time.

In a strict sense, an FM signal is one where the frequency deviation resulting from a constant amplitude modulating signal is the same for all modulating frequencies, whereas a PM signal is one where the frequency deviation resulting from a constant amplitude modulating signal is proportional to the modulating frequency.

Systems are deployed that are not strictly one or the other, eg so-called broadcast FM has pre-emphasis of frequencies above about 2kHz. And to add to the confusion, narrowband communications FM (with 6dB/octave pre-emphasis of frequencies above about 300Hz (ie the entire speech band) is actually PM to air.

Frequency spectrum of an FM wave

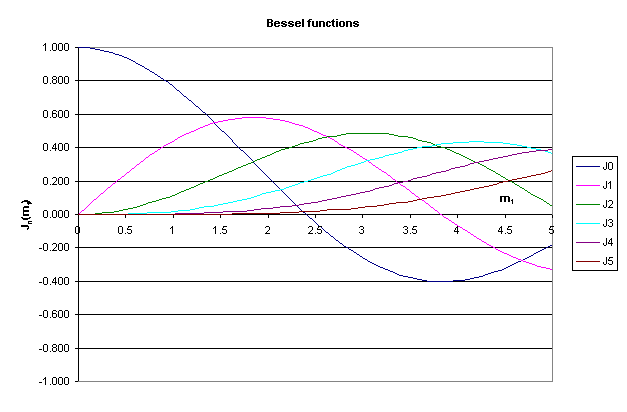
The spectrum of an FM wave is complex mathematically. It consists of a carrier wave with a (theoretically infinite) series of pairs of sidebands. The amplitude of the carrier and each pair of sidebands is given by Bessel functions. Figure 2 shows Bessel function values for the carrier and first 5 sidebands (but realise that it is an infinite series of sidebands. the amplitude of the higher sidebands is very low at low modulation indexes and can be ignored).

Fig 2: Graphical representation of Bessel functions.

Note that as the modulation is increased, the carrier amplitude (J0) decreases to zero at a modulation index of approximately 2.405, and then increases in amplitude (in anti-phase), crossing through zero again at a higher modulation index (approx 5.519).

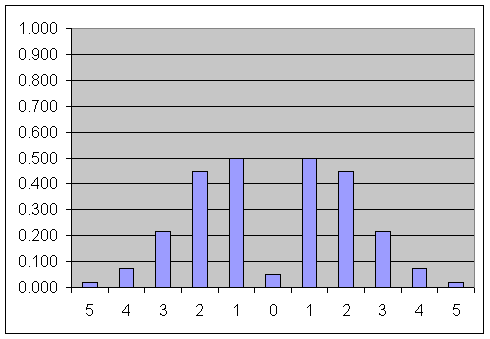
Fig 3: Spectral distribution of an FM wave (mf=2.5).

Fig 3 shows the spectral distribution of an FM wave, The column labeled 0 is the carrier and the other columns are the nth sidebands. Note the large number of sidebands and the carrier (in the centre of the diagram) is near to zero at this level of modulation (modulation index is 2.5). Most (99.7%) of the FM wave energy is in the sidebands.

The values of Bessel functions are commonly published in tables as in Table 1. In the table, mf is the modulation index and J0..Jn are the amplitude coefficients for the carrier and sidebands.

Table 1: Table of Bessel values.
m_f	J₀	J₁	J₂	J₃
0.00	1.000	0.000	0.000	0.000
0.05	0.999	0.025	0.000	0.000
0.50	0.938	0.242	0.031	0.003
1.00	0.765	0.440	0.115	0.020
1.50	0.512	0.558	0.232	0.061
2.00	0.224	0.577	0.353	0.129
2.50	-0.048	0.497	0.446	0.217
3.00	-0.260	0.339	0.486	0.309
4.00	-0.397	-0.066	0.364	0.430

Carson's rule

Carson's rule is often used to estimate the occupied bandwidth of an FM signal. Carson's rule estimates the bandwidth as twice the sum of the peak deviation and the highest modulating frequency.

For example, Carson's rule would suggest that the occupied bandwidth or speech (400Hz - 3kHz) with a peak deviation of 5kHz would be 16kHz.

Noise and frequency modulation

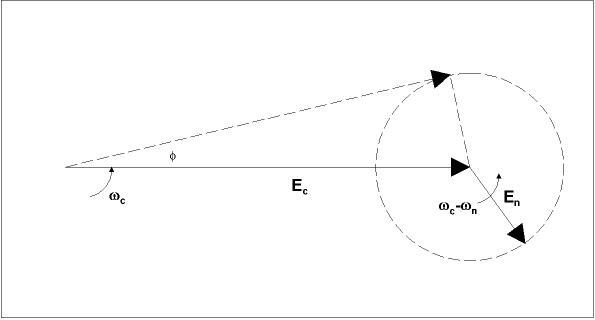
Noise triangle

To understand the effect of noise on an FM signal, it helps to consider a single noise frequency vector added to the FM signal vector (see Fig 4). Since it is at a different frequency, the noise vector will rotate about it with an angular velocity equal to the difference between the noise frequency and the carrier frequency. This will produce a variation in amplitude and phase of the resultant vector. The amplitude variation can be largely eliminated in a limiter stage, but the phase variation (shown as Ø in Fig 4) remains.

Fig4: Effect of a noise phasor on an FM carrier phasor.

The modulation index due to the noise voltage is constant for different noise frequencies, differently to the modulation index for the desired modulation signal which decreases with increasing modulating frequency (for FM). This means that the noise degrades the signal to noise ratio more at higher modulating frequencies. A plot of the noise vs frequency is a triangular shape, hence the term "noise triangle".

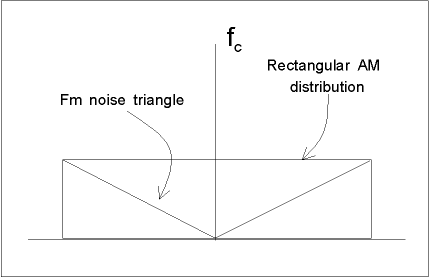Fig 5 shows the distribution of noise sidebands compared with the AM case. The noise power content is only one third (or -4.7dB) that of AM, and the difference improves with higher FM modulation indexes.

Pre-emphasis and de-emphasis

As described, with FM reception, noise contributes more to the high frequency portions of the audio spectrum than to the lower frequency portions. The highs therefore tend to have a lower Signal to Noise Ratio than the lows.

The noise contribution of the high frequency region can be reduced by transmitting the highs at increased relative levels and then reducing the level by the same amount at the receiver. This boosting of the highs at the transmitter is known as Pre-emphasis and the reduction of the highs at the receiver is called De-emphasis.

For realistic reproduction, the amount of de-emphasis at the receiver must equal the pre-emphasis at the transmitter. Simple networks are utilized to achieve this. The networks are typically a single RC filter stage, and are characterised by the time constant of the filter section.

Wideband broadcast applications use a time constant of 50uS or 75uS (Europe or USA).

Narrowband voice applications usually set the filter breakpoint outside the voice band and deliver a 6dB / octave slope over the entire band. This tailoring of the modulation so that the frequency deviation is proportional to the modulating frequency effectively renders phase modulation.

Demodulation

Frequency demodulators were easier to build than phase demodulators (a phase demodulator needs a reference phase), so we tend to fit receivers with FM demodulators. Traditionally, FM detectors were discriminators, which convert the frequency shift to an amplitude change using a specially configured transformer and few other components.

Today, practice is to use quadrature detectors which mix a delayed copy of the input signal with itself to produce a voltage that is proportional to the time delay. A simple tuned circuit is used to create a phase delay that is proportional to frequency and so allow the circuit to produce an output voltage that is dependent on "instantaneous" carrier frequency. Such circuits are combined with IF amplifier and limiter circuits on single chips.

The theoretical signal to noise ratio for FM with modulation index equal to 1 is 4.7dB better than AM as explained by the noise triangle. Apart from the noise triangle benefit, both FM and PM benefit from noise reduction compared to AM because of the angular modulation, and the improvement is 20*log(m) dB where m is the modulation index. To achieve these theoretical benefits, the detector must only respond the phase variations, so any limiter if required must be fully effective.

For narrowband FM systems with 6dB / octave pre-emphasis (effectively PM) operating with m=3 and fully limiting, the FM improvement factor is about 10dB.

Production of FM / PM

Reactance modulator

A simple method of producing FM is to use a variable reactance element (such as a varicap diode) as one of the elements of an oscillator LC tuned circuit. This produces FM quite well.

If we apply this technique to a crystal oscillator, the very high Q of the quartz resonator makes it very hard to pull the frequency. The deviation is achieved is quite small, but may be increased in a frequency multiplier chain.

Another method of producing angular modulation is to apply the modulating voltage to a variable reactance element connected to a tuned circuit later in the transmit chain, where it will produce phase modulation rather than frequency modulation. If we feed audio signals to a phase modulator, the resulting frequency deviation is greater for the higher modulating frequencies than for the lower ones.

We can use a phase modulator to produce FM by compensating for the phase modulator's effect of producing peak frequency deviation that is proportional to the modulating frequency. This is done by passing the modulating signal through a simple RC filter with a 6dB / octave roll-off. The filter is a low pass filter with the cut-off frequency below the lowest desired modulating frequency.

PLL

Modern radio transceiver use a phase locked loop to control a VCO running at the transmit frequency. It is possible to apply modulation directly to the VCO, but the action of the PLL will tend to eliminate the modulation, especially at the lower modulating frequencies (the behavior is dependent on the loop bandwidth of the PLL control loop). Alternatively, the modulation could be applied to the reference, but it is hard to achieve high modulation bandwidth. To overcome this, it is common to feed modulating signal to both the reference oscillator and VCO, and to adjust the balance of these to null the modulating signal in the PLL control loop.

Other systems

FM can be generated by other techniques, such as the Armstrong Modulator or other forms of synchronous modulator, and modern digital techniques have introduced further methods. Frequency modulators for narrow voice band FM are usually variable reactance modulators, and in the case of PLL based radios, applied to the reference oscillator and the VCO.

Applications

Voice - narrow band

Angular modulation is used in narrow band voice applications in Amateur radio. Different configurations are used on HF, and VHF/UHF.

VHF/UHF application is usually FM with a 6dB/octave pre-emphasis over the whole voice band (in effect PM) with a peak deviation of 5kHz. Carson's rule estimates the bandwidth for a 3kHz voice band at 2*(3+5) or 16kHz. This is commonly employed in a 25kHz channel spacing plan.

Sound - wideband

Amateur television transmits the sound on conventional (analogue) TV signals using commercial FM standards for the sound subcarrier.

Digital - FSK

Frequency Shift Keying (FSK) is used on HF for low speed telegraphy or data transmission, eg RTTY at speeds of 45.45 or 50 baud.

FSK is also used on VHF for data transmission at 4800 bps using the HAPN Direct Frequency Modulation (DFM) technique, or G3RUH modulation at 9600bps.

Digital - AFSK

Audio Frequency Shift Keying is the use of a frequency shift keyed audio tone to modulate a FM or SSB transmitter. This is commonly used for speeds of 300bps on HF and 1200bps on VHF/UHF. On VHF/UHF, the AFSK signal is fed into the microphone input of the transmitter to pick up pre-emphasis, and de-emphasised audio is used for the demodulator.

Digital - PSK

Phase shift keying is used for transmission of telegraphy or data at speeds such as 31bps on HF (PSK31).

Applied test and measurement

Measurement of frequency modulation

Calibration of a frequency demodulator

A demodulator is best calibrated to transferring calibration from a calibrated modulator. A procedure for calibrating a modulator follows.

Calibration of a frequency modulator

The usual method of calibrating a modulator is to use the spectral properties of an FM signal.

One could use a spectrum analyser to find the calibration point, adjusting the modulation level and detecting the null of the carrier or sidebands according to the Bessel function.

Since the instrumentation is used to detect the null of a carrier or sideband component, and the null is very sensitive, a narrow band receiver can be used for the calibration procedure.

A practical approach

This is a procedure to calibrate a frequency modulator at a single modulating frequency using an SSB receiver to detect the first carrier zero.

The technique is very sensitive, and error will mostly be attributed to the accuracy of the modulating frequency.

Table 2 shows the mf for the first five carrier zeros, and is a handy reference list for calibration of a modulator.

Demonstration

You have read about it, click to listen to a demonstration. This demonstration uses an SSB receiver with a 3.5kHz IF bandwidth, but I have used the technique with receivers with a 10kHz IF bandwidth, you just hear more of the sidebands, but concentrate on the carrier beat and null it out. The test receiver could be a high quality communications receiver or a scanner with a BFO. You could sample the modulated signal at the carrier frequency, or by sniffing some signal from the IF of a super-heterodyne receiver.

Transferring calibration

Having calibrated a modulator, you could then transfer the calibration to a demodulator. Be wary of audio filtering in receivers, it is probably safer to calibrate discriminator output if you can get it, and make adjustments for de-emphasis manually. Be wary also of filtering at the low end of the audio spectrum, particularly in receivers designed for CTCSS.

Application to VHF packet 1200bps

VHF 1200 bps packet uses Bell 202 standard with a space frequency of 2200 Hz and a mark frequency of 1200 Hz. Terminal mode software such as TAPR V1.8 or Paccom V5 in the TNC offer a CAL command for setting transmit audio level.

Importantly, many TNCs and modems employ a PLL type demodulator (usually chip based). These types of demodulators do not work well when the low frequency tone is significantly higher in amplitude than the high frequency tone.

It is imperative that pre-emphasis / de-emphasis is consistently applied, and that clipping or limiting in the transmitter audio chain post pre-emphasis does not effectively nullify the pre-emphasis.

The desired condition is 3kHz of deviation with the high frequency (2.2kHz) and 1.64kHz (1.2/2.2*3kHz) deviation on the low frequency (1.2kHz).

It should be possible with most transceivers, to achieve a modulation index of 2.405 (first carrier zero) using the mark frequency (low tone /1200Hz) at a deviation of 2.88kHz without onset of audio limiting, whereas audio limiting is quiet likely at the first carrier zero using the space frequency (deviation would be 3.9kHz). This procedure calibrates the modulator using the mark frequency (1200) to achieve initially 2.88kHz deviation and then reducing it to 57% to achieve 1.64kHz deviation.

If in doubt, err on the side of low deviation. Signals with 0.3kHz deviation (ie 20dB low) are quite copy-able even at the micro-volt signal level, whereas signals with too much deviation and / or nullified pre-emphasis are not workable at any strength on narrow receivers using PLL demodulators.